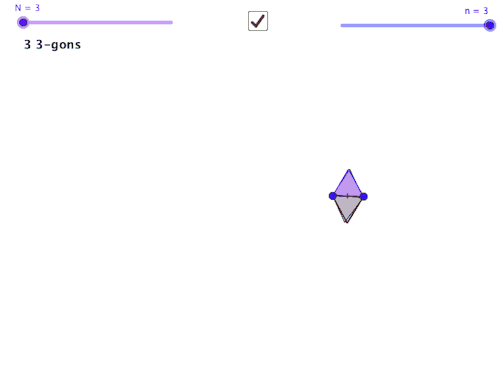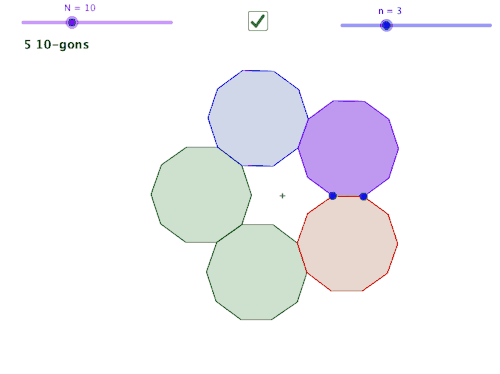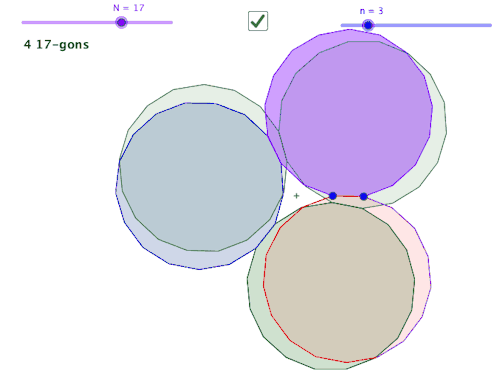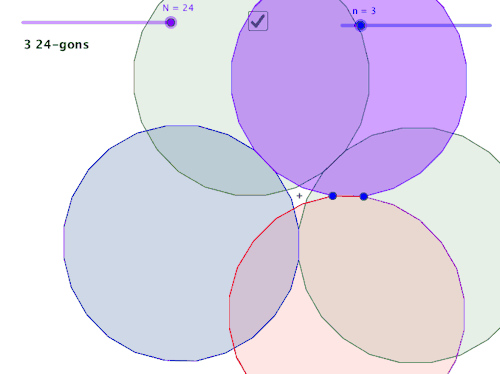
在几何学中，关于构造的单元通常从演示开始，练习复制线段、复制角度、将线段平分、将角度平分。这些被视为构建块，含蓄地承诺稍后进行更详细的构建。实际上，很快，这个单元就会通过一个给定的点构造一条平行线，并通过一个点构造一个垂线。但学习“构建块”往往会陷入不连贯的程序实践中。理由通常是“你以后会需要它”。这不仅让学习者感到非常不满意，而且有时当我们谈到“以后”时，我们也会将该主题视为不连贯的过程。
一个被困在这类课程中的学生一定会想什么！未来充满了令人感兴趣的问题，但现在必须坚持到底。
让我们把有趣的问题带到现在。使用这项技能可以解决哪些问题？
回答距离问题
几年前，我和另一位老师改编了丹·梅耶（Dan Meyer）的一节课，将这些问题归纳为一句话：“指南针测量距离。”湾区大学地图课程计划（PDF）一个问题问：“马林学院离上海外国语大学有多远？”你是怎么做到的？我们可以用尺子，测量地图距离，测量比例尺，然后找出比例。或者，你可以目测天平，或者用你的拇指和手指来接近它的副本。请注意，这两者都与实际的罗盘和直尺结构相似。
如果你在测量比例尺和地图距离，你实际上是在把比例尺段的长度复制到两点之间的一条线上。这是复制线束段构造一开始不要担心他们会伸手去拿尺子，如果没有尺子，问题会更容易。但也要注意，如果我们问尺子与指南针的比较情况，我们可能会进行讨论。给定1英寸，其余的标记就是你用指南针所做的。
这节课还鼓励这样一个概念，即指南针画的圆是指南针中心的等距点集。当然，这是一个圆的定义，但如果我们问“我们现在离Cal或Mills更近了吗？”我们不必跳到垂直平分线，相反，我们可以慢行：所有距离Cal 10英里和Mills 10英里的点在哪里？画了两个圆。距离每个5英里？再绕两圈。距离每个8英里？再绕两圈。一种模式可能开始出现。如果学生们提议在所有这些交点之间划一条线，不要感到惊讶。
建筑课程绘制
在过去的一个月里，我观察到一些教室在做指南针和直尺的介绍。演示完之后，老师可能会说要练习几次。但学生们的论文通常只有指南针标记和草图的仿制品，显然并不是精确的复制品。这可能会让老师感到困惑，因为整个重点是“复制”。但如果学生不这样做，他们并不愚蠢，只是这项任务毫无意义。字面上没有意义，因为它们没有注意到过程的重要属性是什么。程序的重要属性也具有较高的字数与输出比——“将指南针的中心放在线段的一端，将另一端打开到另一端”。
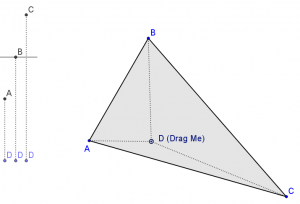
好吧，让我们试着提出一个问题，这样学生就需要复制线段和角度来完成它。我一直在头脑风暴，本质上是“从这里到那里”。第一级显示在左侧。
规则：
- 您只能在BC全程旅行（给定）
- 您只能以FDE的全角度转弯（给定）
- 你可以从任何方向出发
根据这些提示，学生需要复制线段和角度。他们被允许以一种能够激发更多创造力的方式“去”。非正式解决方案（非结构）也是可以接受的，因为在正式化之前尝试一些非正式的方法是完全合理的。
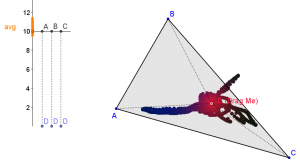
有多种解决方案，但这些点是专门选择的，因此起点和终点不是BC的倍数。学生的解决方案可以通过他们离终点有多近来衡量，这为“更好”的解决方案提供了一些动力，但请注意，他们的施工质量是一个单独的衡量标准。
实际上，我开始这个想法时考虑的是较难的版本：在一张大纸上随机放置两个点，并在中间画出斑点。（见图）给定一个线段和一个角度，你能用它们的副本从头到尾创建一条路径而不碰到斑点吗？
当我想到这一点时，有几件事突然向我袭来。首先，学生们可能会以这种方式复制更多的角度和分段，而不是你在练习中可以轻松指定的。（这很好！）我在思考课程的实施和潜力时写的其他东西
- 该线段应该不同于远离角顶点的线段长度处的角宽度。（真是一团糟——但本质上，这意味着如果线段和角度要求指南针的开口几乎相同，那么它可能会混淆你在指南针中的测量值
- 复制一个片段变得非常简单（哈哈），但有时你需要扩展你的目标线，体验这种需求对学生来说很有价值，因为它很难用语言描述。
- 复制角度需要大量改变指南针-预计会有一些困难（但这是你希望他们克服的）
- 随机放置孤岛可能会阻止解决方案的存在，但会发现这很强大。适应：也许你被允许离开报纸？或…参见#8
- 一个简单的级别（如上面的级别1）可能应该首先完成。需要将其设计为需要每个线段和角度。
- 中等水平就像我在这里画的，或者老师（上课前）先画出解决方案路线，然后放置岛屿来设计水平。
- 硬水平可能是你让学生为彼此设计的水平。这些并不一定很难，但只是难度的差异很大。
- 扩展：如果一个级别特别具有挑战性，你可以“允许”学生平分一段或平分一个角度，并使用一次一半大小的项目。面临这种选择的学生需要评估哪种选择是最好的，因此可能需要练习几次对分技能。
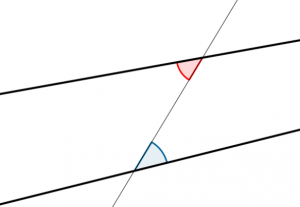
- 平行线结构的元素可以自动生成，因为学生可以在横向或交替的内角上以相应的角度复制角度。
- 说到这里，横截面和平行线上的角度也是这个活动的自然结果。学生们可能会猜测平行线上的全等角，这为你现在或以后提起这个单元提供了一些讨论的素材。
- 单个线段和角度的底层结构是平行四边形网格。这有助于评估解决方案，也可以从它是代数的入口点的角度进行讨论可构造数。这并不是说你需要详细讨论概念，但你可以打下一些基础
此外，我认为学生有足够的机会想出一个给定水平的创造性解决方案。由于第一个方向是任意的，学生们可能会有不同的解决方案，这些都值得庆祝。学生们可以看看彼此的工作，注意到所面临和解决的小问题中的相似之处（绕开一个岛屿），也可以在技能上相互帮助，而这并不是问题的“答案”。学生们可能会有兴趣通过用不同的选择重新做来改进他们的解决方案。我可以想象一堵墙上挂满了几十张学生地图的漂亮墙！
如果你尝试这个想法或与之相关的东西，我很想听听！以下是我已经收到的一些相关资源：
真实
最后，这里的问题的“真实性”并不取决于它们是“真实世界”。它们是真实的，在某种意义上，它们可以通过使用所讨论的技能来回答，也许除了访问先前的知识之外。这与我们所说的“练习三次技能”的假问题形成了对比。主要区别是，真正的问题可以在没有技能的情况下被攻击，但技能可以改进解决方案。假问题直接要求技能，因此它成为唯一可能的解决方案。
你怎么认为？geogebra-applet问题是真的还是假的？我说，距离很近。这个问题的一个更假的版本将为学生完成所有的预处理，直接告诉他们“复制EF”。这是我认为许多建筑课程的倾向。我说，这个问题的真实性来自这样一种感觉，即我可以在不使用指南针和直尺的情况下提供合理的答案，而这些工具肯定会改善我的结果。但是，肯定有一个正确的答案，而构造几乎是正式实现它的唯一方法（如果我们假设勾股定理依赖于构造）。所以，为了让它更真实，我们改变了目标。上面的课程绘图活动是一次大调整：我们必须从头到尾使用复制的线段（和角度），但学生在如何使用这些工具方面有代理权。
这里的目标是指南针和直尺的构造。忘记“我们稍后会需要它”，让“现在就需要它”！
