丹·梅耶前几天在推特上发布了一个“硬币问题”的经典例子。问题出在皮尔逊的共同核心代数2文本。让我们假设皮尔逊的作者在这里选择入选时有积极的意图,因为乍一看,这可能不是很“常见的核心”。但实际上,不管他们的意图如何,让我们看看这类问题(1)传统上把我们带到了哪里,(2)我们可以用它来探索非传统方法。
这篇文章改编自我在丹的帖子中的评论。
马克有42枚硬币,由一角硬币和四分之一硬币组成。他的硬币总价值是6美元。他有多少种硬币?展示你所有的工作,并解释你用什么方法解决问题。
这是什么问题?这通常出现在代数1类中的线性方程组单元中。课文本身是一本代数2的书,所以我们可以放心地假设他们的意图是用它作为一个略带修饰的线条系统练习的例子。
所以我的想法是退一步。(1)它的两个方程和两个未知数——这些有什么有趣和重要的?这是什么样的数学结构?(2)硬币的上下文对我们的结构有什么影响?(3)硬币背景是否增加了我们揭示潜在结构的能力?
简介
想想看,知道你有多少硬币,但不知道每种面额的硬币有多少,这有点奇怪。这是学生学习到的人为背景的最初迹象。大多数是在高中阶段,学生在课堂上形成了一些身份,迫使他们配合老师的指导,所以如果他们最初不感兴趣,他们可能会与你保持一些联系。但也许你班上的一些大言不惭的人会指出这种人为情况的一些奇怪之处#embracetheloudmouth公司
所以,也许在系列课的某个时候,你有机会说,“卢·德茅斯,你完全正确,在什么情况下,我们可以知道硬币的总数和总价值,但不知道它们的分割?”
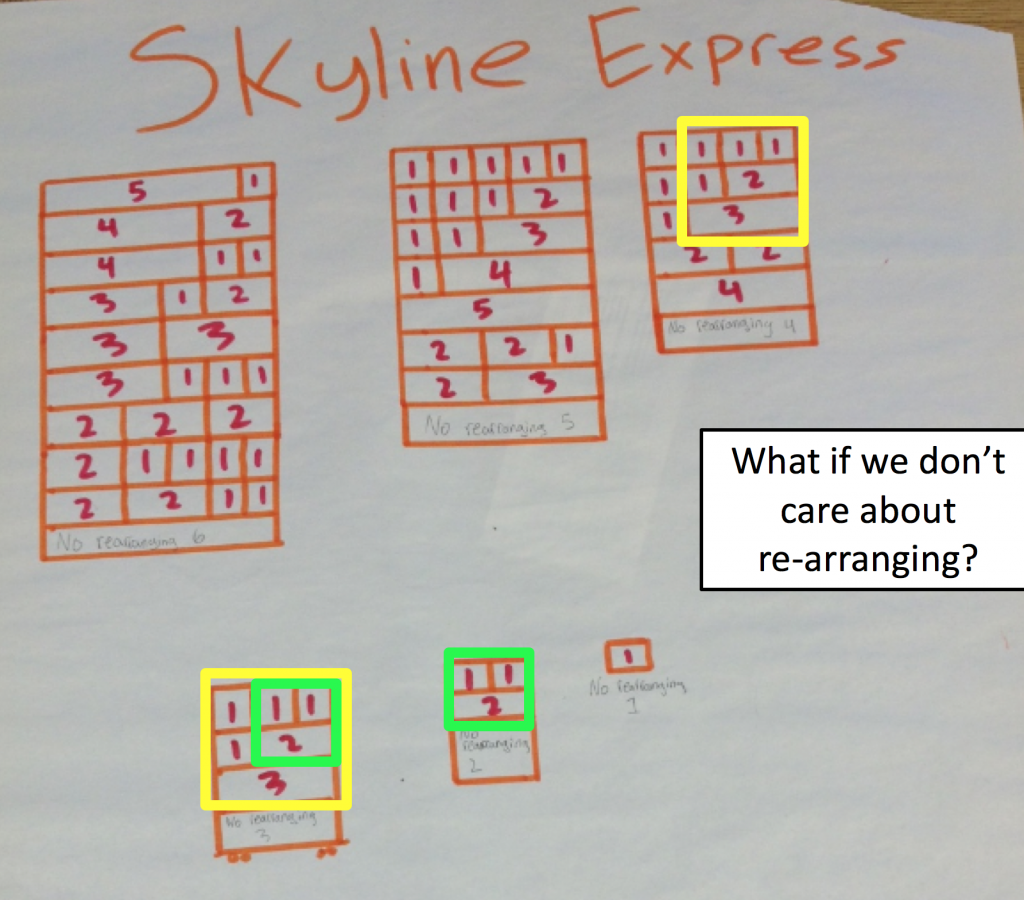
在这里,你可以设置类来解决这个硬币问题。 (子弹!)
让孩子们“获得元”
我喜欢Denise Gaskins的@letsplaymath想法:把它变成一个20个问题的游戏:斯图伸手到硬币罐里抓一把,其他人问Q,看看他们有什么硬币。?
这改变了任务的要求:我们不仅想找到一解决方案,但我们表面上关心的是,就所问问题的数量而言,我们能有多高效地做到这一点。为什么至少要回答两个问题?丹尼斯的活动可能不会持续很长时间,但这没关系,因为学生们为什么会停止?他们会发现这有多容易!他们会全神贯注。也许老师可以明确地要求小组试着问一个问题来回答#of quarters和#of dimes。
(据推测,我们将不允许“多少季度?”尽管我们仍然需要两个问题,这仍然很有趣…)
进一步说明这一部分的问题可能包括:
问:如果你问“多少个硬币?”他们回答“8”,为什么不让我们知道他们手里有多少硬币?
展开结构
现在我们可以承认这个发明,因为它将引导我们了解这个数学结构的特殊之处。我们承认并放松了我们的发明:参数化硬币数量。推特上的一些人在回应丹时,除了我之外,还有这个想法。
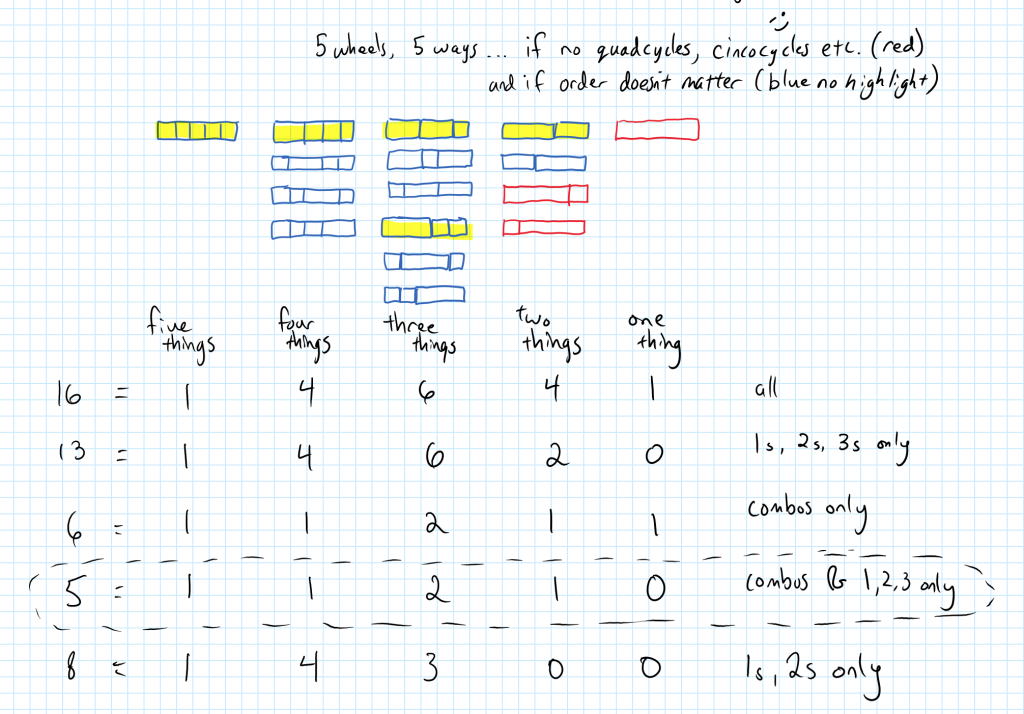
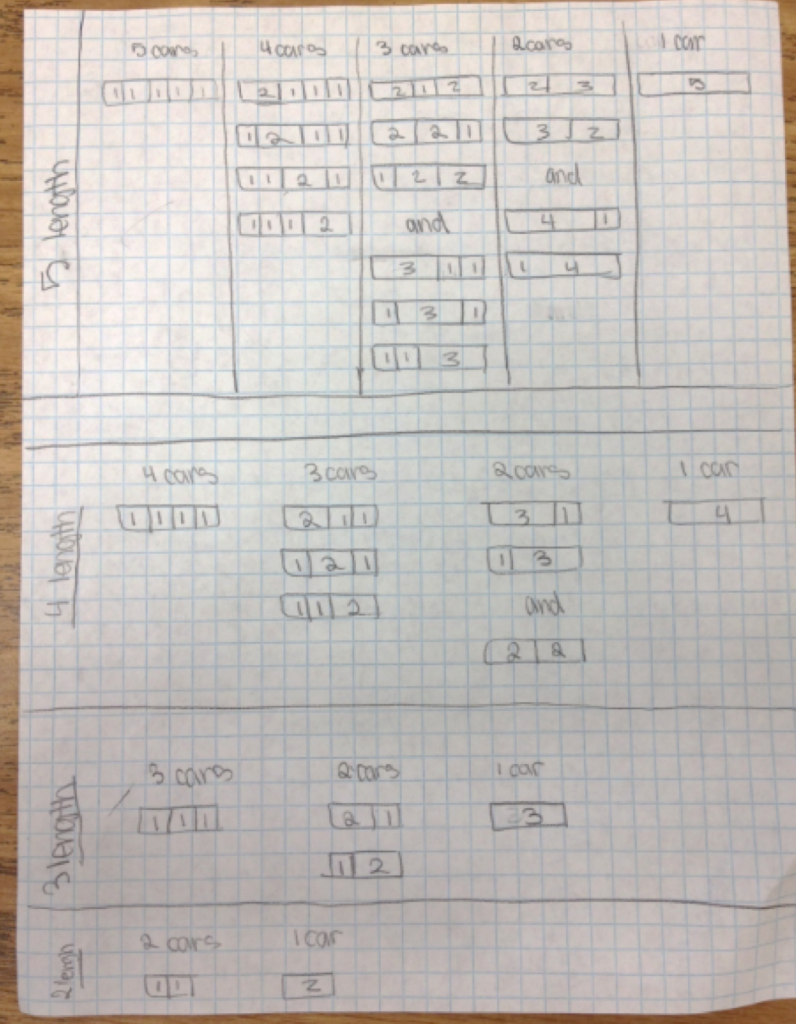
(让我们把数字变小)假设我们有2.00美元,如果我们只使用四分之一和硬币……我们需要多少硬币?N=8个硬币(8q0p)是一种方式…N=104是另一种方式(问怎么回事!)。
1.花一些时间查找Ns。数学实践标准:利用结构!(我们如何知道何时完成?)
2.如果加起来是2.00美元,那么每个N(硬币总数)是否只分为四分之一和一分钱?为什么?
3.为什么一些Ns(例如105)没有任何解决方案?
4.***是什么原因迫使我们有或没有独特的解决方案***
和5。我们是否可以设计一个新词,使$s,N具有多个四分之一penny分区?这可能吗?
回想一下你还是学生的时候
我记得在我自己的教育中有很多手工和“崇拜”,因为两个方程和两个未知数都有解决方案。(以及3等式、3未知等……)
但是,像“好吧,这是2个方程和2个未知数,这样我们就知道怎么做了”这样的语句正是数学魔法书的灵感来源。孩子们觉得那些擅长数学的人知道如何拼写“incent”,如果“2等式2未知数”能让答案无处不在,那一定是一个很好的拼写!
不要解决得太快
我认为这是一种罕见的情况,在这种情况下,我不会很快得到一个图表。是的,我们知道线的交点。是的,我们可以证明这些硬币的关系是线性的。
但是,我们能证明基于#约束的有限解决方案是可以推广的吗?我们从四分之一便士开始。在中间,我们可能会证明一些关于#系统解的东西,我们会讨论其他想法,比如混合物等等。但到最后呢?我们需要学生摸索(http://en.wikipedia.org/wiki/Grok)系统和解决方案的理念。
德霍斯之前的笛卡尔
也许这是老师脑子里想的东西。但是,老师对数学结构的思考越深入、越丰富,学生的想法之间就可以建立更多的联系。在这里,我们可以稍微思考一下笛卡尔平面的天才:
该图告诉我们:
–线性模型的无限性质
–线性模型的单调性
–coinA:coinB和valueA:valueB之间比率的差异(因此斜率不同)
–符合硬币计数条件的所有订购对
–符合总值条件的所有有序对
结合我们对不同角度直线的几何知识,将其映射到线性模型上,并将其映射至硬币情况……这就是我们证明奇异解的方法。
这一切在课堂上的表现可能仅仅是额外的15秒等待时间、小组讨论的额外问题、思考的增量食物…
与其说我们想要一个完整的答案,还不如说我们希望学生承担起辩护的角色。
T、 S:“为什么我们知道这里有一个解决方案……?”
让学生把它带到讨论中
如果S通过图表进行推理,那太棒了!
但S可能会这样说:“如果我们减去一个季度,再加上一个时间,我们会将硬币总数保持在42,但会贬值……我们总是会以这种方式贬值,所以再加上几个季度就没有解决方案了!”
这是(a)矛盾证明和(b)使用适用于函数理论的概念:递减、单调。(在本例中是一个序列)但S也合成了一个假设,该假设推广到了更大的情况:减去四分之一,再加上一角。然后,他们提出这样的任何情况都无法提供解决方案,从而提升了他们的抽象性。(类似的论点也可以用于加25美分,减去1美分)
然后,T有机会让全班同学参与讨论,将图形推理和演绎推理联系起来。
这很可能会成为一个关于为什么笛卡尔图如此伟大的讨论,而且一切都更好!许多学生在绘图方面很费劲,因为他们坚持程序,没有意识到图形在实例中或一般情况下具体代表什么。
跳出文学
在这篇帖子的开头,我提出了这样一个想法:学生会接受一些荒谬的人为情况,因为他们觉得有义务在数学课上遵循某种身份。我在Paul Cobb博士2009年的一篇文章中考虑到了这一点,这篇文章是关于学生在教育过程中如何创建、维护和改变他们的身份。这可能是一件坏事,就像在案例研究课程中一样:
所有学生表达的沮丧和失望表明,他们并没有像在课堂上认识到的那样认同数学活动,而只是与老师合作。(科布,2009年)
P.、Gresalfi,M.和Hodge,L.L.(2009年)。用于分析学生在数学课堂中发展的身份的解释方案。数学教育研究杂志, 40-68.
当我想到课堂讨论时,我喜欢沃尔肖和安东尼2008年关于课堂讨论的论文。最受欢迎的一句话:
除非教师能很好地理解课堂上听到的数学思想,否则他们将无法培养出所需的灵活性,以发现黄金机会和明智的切入点,从而引导学生走向更复杂、更具数学基础的理解。现场反思和处理有争议的数学思维需要良好的教师知识。重要的是,教师管理多种观点的方式在很大程度上取决于他们对数学的了解和信仰,以及他们对数学教学的理解。
Walshaw,M.和Anthony,G.(2008年)。教师在课堂话语中的角色:最近对数学课堂的研究综述。教育研究综述,78(3), 516–551.