目录
目录
想法
对于局部小类别 ,一个预切在或等效a函子
上相反类别属于值在中设置是可代表的如果是的话自然同构的到人-叛徒 ,它发送一个对象到霍姆塞特 在里面

并发送一个同构 在里面到功能发送每个态射到复合材料
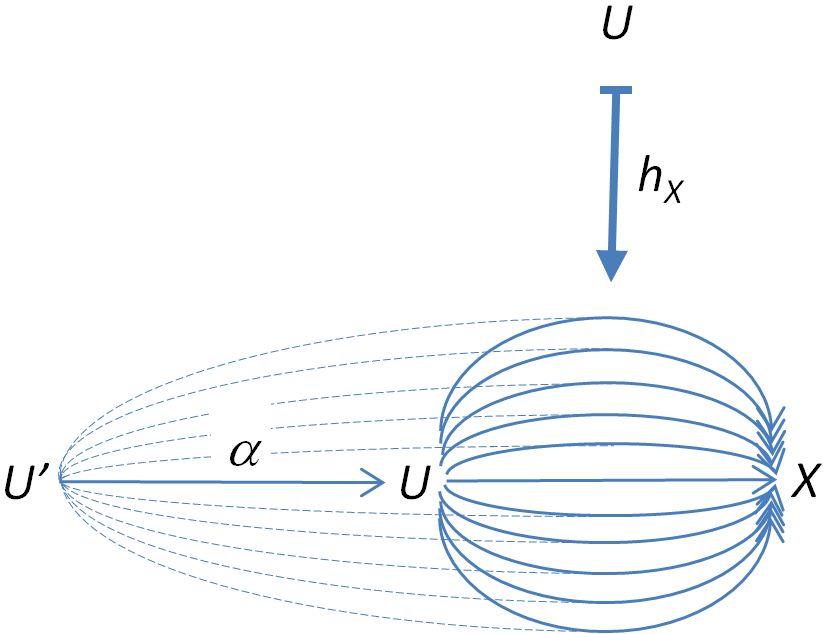
如果我们想象作为如上所述的形态链,然后是形态用于从到,即。
对象是唯一确定的,最多可达同构在里面,称为表示对象对于.
可代表性是范畴理论与伴随函子并发送至米田引理。这是通用属性;因此,例如“限制”, “上极限”, “指数对象”, “Kan扩展“等等都是自然地用表示对象来表达的。这一概念渗透到了代数几何和代数拓扑学中。
定义
在普通范畴理论中
对于函子(也称为预切在),一个表示属于是指定的自然同构
由米田引理,任何此类转换(同构与否)由元素唯一决定如上所述,对象被称为表示对象(或者经常,通用对象)的、和元素被称为通用元件对于。同样,它来自米田引理那一对是唯一确定的,直到唯一同构。
根据Yoneda引理的证明,可表示性正是指:给定任何对象属于和任何元素,存在唯一的态射这样,函数带有通用元件到这样一个干巴巴的公式并没有传达出这一概念的非凡力量,只有通过无数的例子来说明这一点。
抽象地说,是一种预兆当且仅当它允许相对于的左伴随函子来自终端类别,选择终端对象在里面设置.表示对象是通过在唯一对象处计算左相对伴随来给出的.
在丰富范畴理论中
上述定义直接概括为丰富范畴理论.
让成为闭单群范畴和一-丰富的类别.
然后针对每个对象有一个-富足函子
从到通常被视为-丰富的类别.
这是定义的
成为辅助合成态射
A类-富足函子是可代表的如果有和a-富集自然转化 .
如果是对称单体可以形成相反类别 对可表示函子有类似的定义.
在高等范畴理论中
可表示函子的概念在高等范畴理论.
在同伦型理论中
讨论范畴理论 同伦型理论:
命题
(可代表性只是一个命题)
如果是一个单价类别,则类型“F是可表示的”是纯粹命题.
这是中的定理9.5.9HoTT手册.
证明
根据定义,“F是可表示的”只是结束。自是推论9.5.7在HoTT书中的嵌入(参见米田引理),这种纤维只是一个命题。
示例
关于可表示函子示例的中心点是:
可表示函子无处不在.
在相当程度上,范畴理论都是关于可表示函子和其他函子通用结构:Kan扩展,伴随函子,限制,这些都是可表示函子的特例,而可表示函元是这些函子的特殊情况。
在中列出了可表示函子的示例范畴理论很像列出的示例完整的中的分析:可以而且确实可以用这些来填满书籍。(事实上,这个类比比普通人看到的要多:看共同(coend)更多信息)。
记住这一点,我们确实列出了一些特殊情况和特殊类别的示例,这些示例非常有用。但任何列表都必然是极其不完整的。
限制
如果是一个图表在里面,我们得到一个图在中函子范畴(预切类别)作为配咖喱人-叛徒 (该Yoneda嵌入). 反对者的态度限制此图的设置也就是函子发送对象到作为图表极限的集合,在该图中是可表示的在中有一个限制;事实上,该极限函子的表示对象正好是,然后我们获得自然同构
(请参阅hom-functor保持极限).
产品
例如产品,让成为…的对象,并考虑家庭主妇
也就是说,接受对象的函子属于到集合.一种产品正是这个预设的代表或通用对象,其中通用元素正是一对投影映射
我们让读者检查一下这里的可表示性是否恰好意味着给定一对地图
中存在唯一的元素,表示,因此
加权限制
上述示例有一个重要的简单概括。
注意函子上的极限只是圆锥体s结束谁的小费是重点
上述表达式可以等效地重写为.替换此表达式中的常量终端函子由任何其他函子引出加权限额,如上所述。
指数对象
假设是一个允许有限乘积的范畴;给定对象,考虑一下预处理
此预兆的代表或通用对象是指数对象 ;通用元件
是一个名为评价地图.
分类捆绑包
考虑一个类别“nice”空间(只是为了解决讨论问题,让我们说仿紧空间,尽管这是一个技术点)和拓扑组其中,即.有预兆
分配给每个空间的同构类的集合-捆束超过,并指定给每个连续映射函数
携带(a类)-束回拉束的(类)众所周知,拉回结构对于同伦变形是不变的;也就是说,这个前缀下降到同伦范畴,
A类分类空间 正是这个函子的表示对象;通用元素是(同构类)分类-束.
这些一般性的考虑在代数拓扑学中非常常见,例如在广义上同调理论和谱之间的联系中;参见Brown的可表示性定理。
工具书类
早期账户:
关于可表示函子的讨论丰富范畴理论在第1.6节和第1.10节
对可表示函子和函子表示之间的差异进行了查询讨论在这里.

