目录

想法

• A类函子是一个同态属于类别.

• 介于之间的函子小类别是一个同态的潜在的 图尊重作文属于边缘.

所以，对于$C$,$D类$二类别，函子$F\冒号C\至D$包括

1. 一个组件-功能的类属于物体;

   $F_0\冒号对象（C）\到对象（D）$

• 一个组件-功能属于套属于态射

  $F_1\结肠Mor（C）\至Mor（D）$

  或同等方式：

  对于每个一对 $x、 对象（C）中的y\$属于物体，一个组件-功能

  (1)$$F_{x，y}\；\冒号\；C（x，y）\xrightarrow{\；\；}D（F（x），F（y））$$

  之间家庭成员;

这样：

• 它尊重来源和目标属于态射:$F_1级$与…一致$表格_0$关于源对象和目标对象；

• 它尊重同一态射:$F（id_X）=id_{F（X）}$;

• 它尊重作文：两个态射合成的图像$F类$是他们图像的合成。

这最后两个性质是函子的决定性性质；他们被称为函数性条件这些是对同态（第页，共页幺半群,组,代数等）的情况下，有更多的对象。作为口号：

函子的概念是水平分类的同态.

定义

外部定义

A类函子 $F类$来自类别 $C$到一个类别$D类$是一张地图发送每个对象 $x\单位：C$到一个对象$D中的F（x）$和每个同构 $f:x\到y$在里面$C$到同构$F（F）：F（x）至F（y）$在里面$D类$，因此

• $F类$保存作文:$F（g \大约F）=F（g）\大约F（F）$只要左侧定义明确，

• $F类$保存同一态射：对于每个对象$x\单位：C$,$F（1_x）=1_{F（x）}$.

或等效，因为成分$g f=g \circ f$（交换三角形）和恒等式$1_x（1_x）$（换向回路）都是简单的换向图，我们可以将上述条件组合成一个语句

• $F类$保存换向图.

鉴于态射 $f\冒号X\到Y$,$g\冒号Y\到Z$、和$h\冒号X\到Z$，声明三角形通勤等于声明

在这种情况下，对于$F： C\到D$保持交换三角形意味着

如下所示

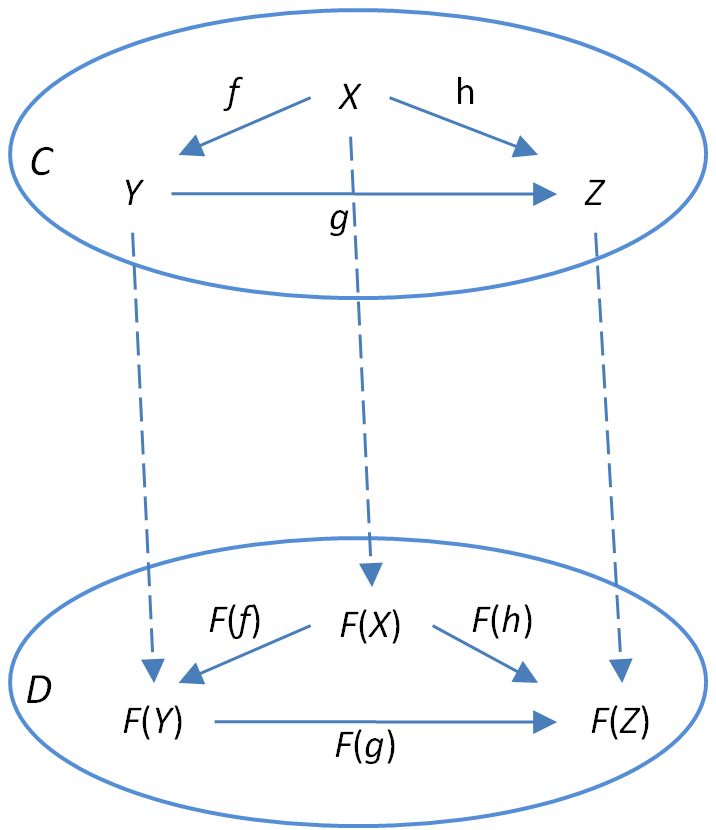
保留交换三角形意味着$F类$保存成分。

给定的形态$f： X到Y$,$g： Y到Z$、和$h： Z\到X$，声明循环通勤等于声明

在这种情况下，对于$F： C至D$保持交换环路意味着

如下所示

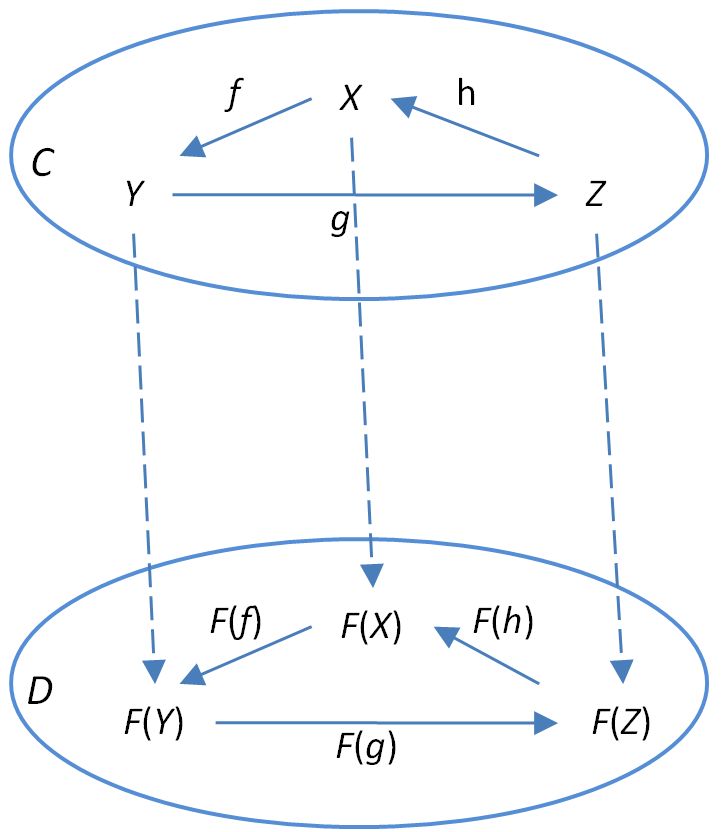
然而，这意味着更多。由于任何交换循环都等于恒等式态射，我们还必须

暗示

保留通勤环路意味着$F类$保留身份形态。

另一种等价的说法是函子$F:C\至D$正是单纯形集 $N（F）：N（C）至N（D）$在神经这些类别中的

• 这个物体属于$C$和$D类$是的0个单元格$N（C）号$和$N（D）号$，所以$N（F）_0:N（F$映射对象$C$到的对象$D类$;

• 这个态射属于$C$和$D类$是的1个单元格$N（C）号$和$N（D）$，所以$N（F）_1:N（F$映射的形态$C$到的对象$D类$;

• 的同一态射$C$和$D类$是的退化1-细胞$N（C）号$和$N（D）号$，所以事实是$N（F）号$尊重简并映射意味着$F类$尊重身份；

• 的交换三角形$C$和$D类$是的2个单元格$N（C）号$和$N（D）号$，所以事实是$N（F）号$将2个单元格映射到2个单元格意味着它尊重交换三角形，因此它尊重合成。

请参见神经有关此的更多详细信息。

两个范畴之间的函子$C$和$D类$形成一个类别函子范畴 $[中、日]$，其形态是自然变换。将这些函子类别作为人-物体，我们有一个$2$-类别 猫范畴、函子和自然变换。换句话说，函子是态射在里面$猫$.

内部定义

如果$C$和$D类$是内部类别在某些环境类别中$A类$，然后是内函子 $F:C\至D$是

• 对象的形态$F_0:C_0\至D_0$在里面$A类$;

• 语素的语素$F_1:C_1\至D_1$在里面$A类$;

• 这样，下列图表就可以相互转换

  • 对源地图的尊重：$\阵列{C_1&\stackrel{f_1}{\to}&D_1\\\向下箭头^s&&\向下箭头^s\\C_0（0）&\stackrel{f0}{\到}&D_0}$;

  • 尊重目标地图：$\阵列{C_1&\stackrel{f_1}{\to}&D_1\\\向下箭头^t&&\向下箭头^t\\C_0（0）&\stackrel{f0}{\到}&D_0（0）}$;

  • 尊重身份$\阵列{C_0&\stackrel{f_0}{\to}&D_0（0）\\\向下箭头^i&&\向下箭头^i\\C_1&\stackrel{f_1}{\to}&D_1}$;

  • 尊重组成$\阵列{C_1\时间{t，s}C_1&\stackrel{f1\times_{t，s}f1}{to}&D_1\时间{t，s}D_1\\\向下箭头^｛\circ｝&&\向下箭头^｛\circ｝\\C_1&\stackrel{f_1}{\to}&D_1}$.

这再现了上述函子的外部定义小类别，属于类别内部到 设置

在许多情况下，这一概念过于严格，我们应该使用内部算符而不是。

丰富的定义

在丰富范畴理论函子映射不家庭成员但给定的人-物体以尊重其构成的方式相互交流。详见

• 富足函子.

Profunctors函数

概念的概括富足函子是的概念亵渎者.

高范畴函子

在高等范畴理论函子有相应的更高的概念，例如

• 2-函子

  • 严格2-函子

  • 伪函子

  • 松弛函子

• （∞，1）-函子

• 另请参阅关于函子的实验替代定义.

在同伦型理论中

注：HoTT手册调用类别a“前类别”和a单价类别一个“类别”，但这里我们将分别指“类别”和“单价类别”的标准术语。

同伦类型理论中函子的定义是普通函子的直接翻译。然而单价类别允许我们构造一些这样的函子，在经典数学中需要选择公理或使用算符.

让$A类$和$B类$是类别.非正式地函子 $F:A\至B$包括

• 一个函数$F_0:A_0\至B_0$
• 对于每个$a、 b:答$，一个函数$F_{a，b}：hom_a（a，b）\到hom_b（F a，F b）$，通常也表示$F类$.
• 对于每个$a： a类$，我们有$F（1_a）=1_{F a}$.
• 对于每个$a、 b、c:a$和$f： hom_A（A，b）$和$g： hom_A（b，c）$，我们有

形式上$A类$到$B类$是

中的形式定义Coq公司可以在中找到Ahrens-Kapulkin-Shulman阿伦斯·卡普金·舒尔曼13.

属性

这些属性来自HoTT手册.

通过感应开启身份，函子也保留$伊多索$（请参见类别).

函子的合成

对于函子$F： A\至B$和$G： B至C$，它们的复合$G\circ F:A至C$由提供

• 复合材料$（G_0\circ F_0）：A_0\至C_0$
• 对于每个$a、 b:答$，复合材料
  $$（G_{Fa，Fb}\circ F_{a，b}）：hom_a（a，b）\到hom_C（GFa，GFb）$$

HoTT书中的引理9.2.9

函子的合成是结合的$H（G F）=（H G）F$.

证明：由于函数的组合是关联的，因此对对象和homs上的动作来说，这是立即发生的。由于hom-set是设置好的，其余的数据都是自动的。$\正方形$

HoTT书中的引理9.2.10

引理9.2.9是连贯的，即以下等式的五边形对易：

函子的类型

特定类型的函子在应用中很重要。请参见示例

• 本质满射函子

• 全函子

• 忠实函子

• 完全忠实函子

有关更多背景信息，请参见材料、结构、财产.

示例

幺半群和群的形态

对于$A、 B类$ 幺半群或$G、 H（H）$ 组，让$\马特布夫{B} A类，\mathbf{B} B类$,$\马特布夫{B} 克$,$\马特布夫{B} H（H）$是对应的一个对象类别（如所述去耦). 然后是函子

是具有单胚同态的正则双射$A\至B$以及相应的函子

具有群同态的规范双射$G至H$.

陈述

使用$\马特布夫{B} 克$如上所述，上的函子$\马特布夫{B} 克$值在中兽医与线性相同表示的组 $G公司$事实上，我们有范畴的规范同构

的函子范畴表示类别。

线性贴图

让$\mathbf{B}端（U）$和$\mathbf｛B｝结束（V）$是单对象范畴，其对象是每个有限维向量空间，且其形态都是线性的自同态在那个空间，即一个物体上完整的子类别属于$Fin Vect公司$.

左反转

如果线性映射$F： U到V$有一个左反转，即。

哪里$F类^*$是前映像，然后我们可以构造一个函子

通过定义其对对象的操作

哪里$F类_*$右边是形象及其对自同态的作用

成分紧随其后

由于对于任何向量，都保留了身份态射$年$在里面$F_*U\子集V$，然后

对于某个向量$x个$在里面$U型$我们有

以便

根据需要。因此，$F类_*$是一个函子。

右反转

如果线性映射$F： U到V$有一个右反转，即。

哪里$F类^*$是前像，那么我们可以构造一个函子

通过定义其对对象的操作

哪里$F类^*$右边是前像，它对自同态的作用是

成分紧随其后

由于对于任何向量，都保留了身份态射$x个$在里面$F^*V\子集U$，然后

对于某个向量$年$在里面$V（V）$我们有

以便

根据需要。因此，$F类^*$是一个函子。

预升

函子$F:C\设置$值在中设置也被称为预升.正如人们所说的那样相反类别 $C^{op}$属于$C$。请参阅预切了解更多信息。

函数和广义元素

对于$C$一类别、和$X \单位：C$一个对象、和$U型$任何其他对象同构 $x:U\到x$可以被视为广义元素属于$X$，已写入$x中的x$（对于应用于类别的此语言设置共个集合，请参见ETCS系统一般情况见类型理论).

这个设置对象的广义元素$X \单位：C$因此是家庭成员 $\coprod_{U\ in C}Hom_C（U，X）$.

当a同构 $f:X\到Y$在任意类别中$C$我们根本不需要把它作为集合的函数，它总是导出集合的函数广义元素：它发送广义元素$x:U\到x$属于$X$到广义元素

属于$Y（Y）$，使用同态的合成$（f）$用同态$x个$在里面$C$.

根据这种表示法，函子上的函数性条件$F:C\至D$，这是

显示为

如下图所示

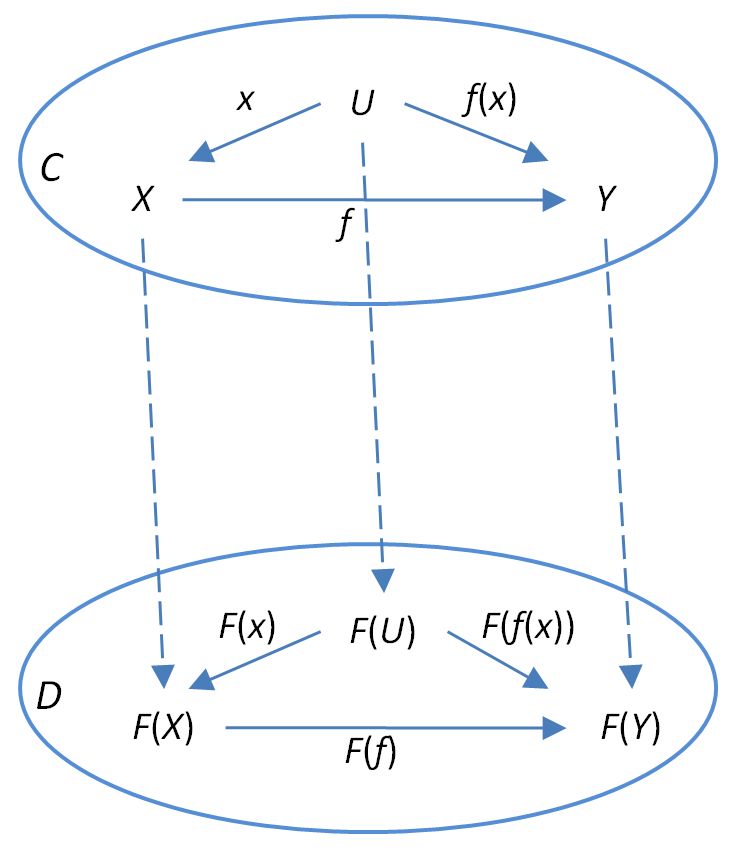
它提供了函数条件的另一种表达方式，即简单地将图转换为$C$映射到中的通勤图$D类$.

相关概念

• 内函子

• 分叉器

• 亵渎者

• 多发性

• 功能

• 函子

  • 内函子

  • 多项式函子

• 2-函子/伪函子

  • 单体函子

• n函子

• （∞，1）-函子

• （∞，n）-函子

工具书类

教科书帐户：

• 桑德斯·麦克莱恩第I.3节：数学工作者的范畴，数学研究生课程5施普林格（1971年，第二版，1997年）[doi:10.1007/978-1-4757-4721-8]

• 弗朗西斯·博尔塞克斯，第1.2节：范畴代数手册第一卷：基本范畴理论[doi:10.1017/CBO9780511525858]

另请参阅以下参考：

• 范畴理论-参考.

• 安德烈·乔亚尔的CatLab：函子

同伦型理论中的函子

• Benedikt Ahrens公司,克里斯·卡普尔金,迈克尔·舒尔曼，第4节单价类别和Rezk完成，《计算机科学中的数学结构》25.5（2015）：1010-1039(arXiv公司：1303.0584)

• 单价基础项目，第9.2节同伦类型理论——单叶数学基础国际会计准则2013

Coq公司将函子概念形式化的代码包括以下内容：

• functors_transformations。v（v）

形式化立方Agda:

• 1个实验室,函子