本页是关于数学.对于中的同名概念哲学请参见范畴（哲学）.

目录

想法

• 类别由事物的集合和它们之间的二元关系（或转换）组成，因此这些关系可以组合，并包含“身份”关系“与相同”

• 类别是指颤抖（a）有向图具有多个边），并有一条规则说明如何组成两条边配合在一起形成新边。此外，每个顶点都有一条从该顶点开始到该顶点结束的边，该边充当此合成的标识。

• 类别是一个组合模型，用于有向空间–a“直接同伦1型“在某种意义上。它有“点”，称为物体，以及连接这些点的定向“路径”或“进程”，称为态射.有一条规则用于如何组成路径；并且对于每个对象都有一个从那里开始和结束的身份路径。

• 更准确地说，类别由物体和一系列态射.每个态射都有一个来源对象和目标对象。如果$（f）$是一个同态$x个$作为其来源和$年$作为它的目标，我们写

  $$f:x\到y$$

  我们这么说$（f）$是来自的态射$x个$到$年$。在一个类别中，我们可以组成同态$g:x\到y$和一个态射$f:y\到z$得到一个态射$f\circ g:x\到z$组合是结合的，并且满足左右单位定律。

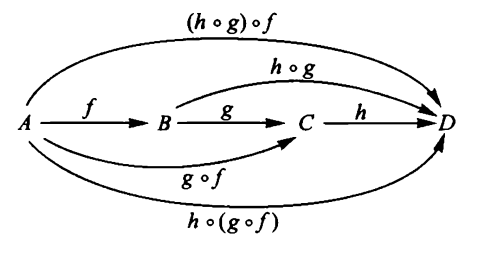
要记住的一个好例子是类别设置，其中对象是集合和同构$f:x\到y$是集合中的函数$x个$到集合$年$这里的组合是函数的常用组合。

有关类别的更多背景和上下文，请参阅

• 范畴理论.

定义

写下范畴的定义有两种大致的方法；像往常一样数学基础，这两个定义是等价的。出于以下几个原因，最好能同时了解这两者：

• 每一个都介绍了自己的记法系统，这两个系统在范畴论的其他部分都很有用，所以人们应该知道它们。

• 一个定义很好地概括了内部类别而其他人则很好地概括了丰富的类别; 这两个概念都很重要。

• 在检查替代基础时，有时一个定义或另一个定义可能更合适；在任何情况下，人们都会想研究它们的等价性问题。

这两个定义可以通过是否使用所有定义的单个集合来区分态射或几个语态集合收藏品系列按成对索引物体.

有一组形态

[格罗森迪克61，第4节]

A类类别 $C类$包括

• 一收集（请参见基础问题和尺寸问题)$C_0（0）$属于物体;

• 收藏$C_1$属于态射（或箭头)；

• 对于每个态射$（f）$，一个对象$秒（f）$（称其为来源或领域)和一个对象$t（f）$（称其为目标或密码子)；

• 对于每一对形态$（f）$和$克$，其中$t（f）=s（g）$，一个态射$g \圈f$，打电话给他们混合成的（也写了$克/平方英尺$或者有时$f；克$-参见图解顺序)；

• 对于每个对象$x个$，一个态射$标识_x$（或$1_x（1_x）$)，调用了同一态射在$x个$;

• 从而满足以下特性：

  • 来源和目标受到成分的尊重：$s（g\circ f）=s（f）$和$t（g\circ f）=t（g）$;

  • 来源和目标受到身份的尊重：$s（1_x）=x$和$t（1_x）=x$;

  • 成分是相联的:$（h循环g）循环f=h循环（g循环f）$无论何时$t（f）=s（g）$和$t（g）=s（h）$;

  • 成分满足左右单位定律：如果$s（f）=x$和$t（f）=y$，然后$1_y\circ f=f=f\circ1_x$.

人们也经常写作$x\单位：C$而不是$x\在C_0中$作为一种简短的方式来表明$x个$是的对象$C类$也有人写$Ob（C）$和$摩尔（C）$而不是$C_0（0）$和$C_1$一个人通常会写$f\冒号x\到y$如果$C_1中的f$声明$s（f）=x$和$t（f）=y$最后，人们经常写作$hom（x，y）$,$hom_C（x，y）$，或$C（x，y）$用于语态集合$f\冒号x\到y$.

如果身份-赋值映射及其公理被省略，然后人们谈到半范畴.

有一个态射集合族

A类类别 $C类$包括

• 一收集（请参见基础问题和尺寸问题)$C_0（0）$属于物体;

• 每对$x、 年$对象的，集合$C_1（x，y）$属于态射从$x个$到$年$;

• 对于每对形态$（f）$在里面$C_1（x，y）$和$克$在里面$C_1（y，z）$，一个态射$g \圈f$在里面$C_1（x，z）$，打电话给他们混合成的（也写了$克/平方英尺$或者有时$f；克$-参见图解顺序)；

• 对于每个对象$x个$，一个态射$标识_x$（或$1_x（1_x）$)英寸$C_1（x，x）$，调用了同一态射在$x个$;

• 从而满足以下特性：

  • 组成为相联的：每四个$w、 x、y、z$对象的数量，如果$f\在C_1（y，z）中$,$C_1（x，y）中的g$、和$h\在C_1（w，x）中$，然后$（f\circ g）\circ h=f\circ（g\circ h）$;

  • 成分满足左右单位定律：对于每对$x、 年$对象的数量，如果$C_1（x，y）中的f$，然后$1_y\circ f=f=f\circ1_x$.

人们也经常写作$x\单位：C$而不是$x\在C_0中$作为一种简短的方式来表明$x个$是的对象$C类$也有人写$Ob（C）$而不是$C_0（0）$和$hom（x，y）$,$hom_C（x，y）$，或$C（x，y）$而不是$C_1（x，y）$一个人通常会写$f\冒号x\到y$声明$C_1（x，y）中的f$最后，人们经常写作$C_1$或$摩尔（C）$对于不相交联合 $\C_0}中的双联体_{x\$.

两个定义之间的等价性

给定一个形态集合类别$C_1\右箭头C_0$，我们通过取$C_1（x，y）$成为前映像属于$（x，y）$在功能 $（s，t）：C_1\到C_0\次C_0$相反，给定一个态射范畴的集合族，我们通过取$C_1$成为不相交联合语态家族的$C_1=\coprod_{x，y\在C_0}C_1（x，y）中$.使用简单的定义函子和自然转化在这两种情况下，都会设置严格的2-等效？属于2类.

但请注意，这个2-等价并不是同构因为不相交并集操作必须用域和余域“标记”每个态射。似乎最有力的一点是物质集合论，如果是集合族的形态范畴$C类$具有设置的属性$C_1（x，y）$都是不相交的，则有一个具有$C_1=\bigcup_{x，y\在C_0}C_1（x，y）中$（该不-不相交的联合）导致$C类$在鼻子上。概念原范畴是一种形式化集合族-形态类别及其hom-set“重叠”的信息的方法。

在普通范畴理论中，人们很少指定使用这两个定义中的哪一个，尽管语言通常隐含地暗示是后者，例如，当定义一个范畴时，首先指定对象，然后指定“来自$X（X）$到$Y（Y）$而不是指定什么是“态射”，以及每个态射的域和余域是什么。事实上，当以这种方式定义一个类别时，人们很少担心hom-set是否不相交，这意味着它必须是使用中的第二个定义。甚至对于原型范畴设置，如果建造在材料集理论基础上，如ZFC公司，自然定义“来自$X（X）$到$Y（Y）$是一个函数，即$X\乘以Y$这是完全和泛函的”，产生了不相交的hom集，因为有序对的完全和泛函集可以具有作为其范围的超集的任何共域。此外，范畴结构并不“自然地”保留homset的不相交性，例如在元素类别 $埃尔（P）$函子的$P： C\设置$中的给定态射$C类$可以是$P（P）$，类似地，对于切片类别等等。

基础问题

我们说，一个类别有一个对象“集合”和一个或多个形态“集合”。然而，不同的是数学基础对…有不同的概念平等.对于其“集合”概念命题-值相等，例如集合论,班-集合论，或伸展型理论，上面的两个定义足以定义一个类别。然而，在其他基金会中，平等观念较弱，例如内部在一个（2,1）-拓扑喜欢Grpd公司，英寸托马斯·斯特里彻的类型的广群模型，或在同伦型理论，一个类别有多种定义。上面用对象集合和态射集合对类别的天真定义导致野生类。如果同构集合是集，则生成的结构是前范畴，如果对象集合也是一个集合，则生成的结构是严格类别集合论基础中的上述定义与替代基础中的严格范畴相同，但在替代基础中，如设置不是严格的类别。相反，它们恰好是一种特殊的预分类，称为单价类别，其中对象的相等是对象的同构。

尺寸问题

我们说，一个类别有一个对象“集合”和一个或多个形态“集合”。一个类别被称为小的如果这些集合都是套-与…相反适当的类例如。（备选方案取决于数学基础.)

类似地，类别是局部较小如果$C_1（x，y）$是每对对象的集合$x、 年$在该类别中。最常见的类别激励示例（例如设置)都是局部较小但不小的（除非有人以某种方式限制其对象）。

替代定义

出于某些目的，改变类别的普通定义的表达方式是有用的或必要的。请参见

• 类别的单排序定义–第一个定义的变体，只有一完全收集($C_1$，没有$C_0（0）$). 出于技术原因，这有时很方便。

• 类别的类型理论定义–第二个定义的变体，在依赖型理论.

• 原范畴–两种定义的混合，其中所有的hom集$C_1（x，y）$是单个集合的子集$C_1$，但不一定不相交。

等效定义

A类类别是等价的

• 一单子在中2类属于跨度属于套;

• 一幺半群在中单体范畴一组物体上的内窥镜；

• 一单纯集合满足西格尔条件;

• 一单纯集合满足弱Kan复合体严格条件：

• 因此a定向同伦型它是“1-截断的”

概括

内部类别

第一个定义，具有单个集合$C_1$语态的概念内部类别本质上，我们定义了一个内部类别（其他类别）$D类$如上所述，“collection”解释为的对象$D类$和“函数”被解释为$D类$特别是设置与小类别是一样的。

丰富的类别

类别的第二个定义，如族$C_1（x，y）$对语态集合的概括丰富的类别：我们定义了一个丰富的类别（其他类别）$D类$如上所述，对象集合仍然是以前的“集合”，但对象为$D类$代替语素和语素的集合$D类$取代了各种功能。特别是，一个类别丰富了设置与本地的小类别是一样的。

索引的类别

概念索引类别捕捉到了在除设置.

多类别等。

范畴的概念有一个泛化，即允许一个态射从多个对象变为单个对象。这被称为多类别或操作的。如果我们另外允许态射到几个对象，我们得到一个多类别或PROP公司.

更高类别

请参见高等范畴理论.

示例

有一个开始类别数据库列出众所周知的类别（如果存在这些类别上的文章，则带有指向这些类别上文章的链接）及其某些属性。

类别的经典示例是设置，具有的类别设置s作为对象和功能s作为语态，函数的通常组合作为组合。以下是一些其他著名的例子，它们是这个主题的变体：

• 兽医-向量空间s作为对象，线性映射作为形态。

• 组-组s作为对象，同态作为态射。

• 顶部-拓扑空间s作为对象，连续函数作为形态。

• 差异-光滑歧管s作为对象，平滑贴图作为变形。

• 戒指-戒指s作为对象，环同态作为态射。

请注意，在所有这些情况下，形态实际上是特殊类型的函数。这些是混凝土类别一般情况下不一定是这样！

这些经典的例子是术语“类别”的最初动机：上述所有类别封装了一种“数学结构”。这些通常被称为“具体”类别（该术语也有一个技术定义这些例子都满足）。但是，与这些类别的分类示例一样，其他类别（通常是“小的“ones），大致来说，它的模型类似于状态和过程某些系统的。

• 姿势A类偏序集可以认为是一个范畴，它的元素是对象，每个元素都有一个态射$hom（x，y）$如果$x个$小于或等于$年$，但没有其他。

• 组A类组只是一个范畴，其中只有一个对象，所有的态射都有倒数-我们称这些态射为群的“元素”。这可能看起来很奇怪，但实际上这是一个非常有用的观点。这里有另一种说法：组是指广群使用单个对象.

• 单体一般来说，a幺半群是具有单个对象的类别。事实上，这是激发类别概念的一种方法：类别是多对象版本关于幺半群。

• 团块A类广群是一个类别，其中所有的形态都是同构第条。

• 颤抖A类颤抖可以用自由类别在其上有向图.给定一个有向图$G公司$包含顶点集合$G_0（G _ 0）$和边缘集合$G_1级$，这是自由的类别 $F（G）$关于其对象集合与顶点集合重合，且其态射集合由中的有限条边序列组成的图$G_1级$头尾相接。这个自由类别中的合成操作是边序列的串联。

• 通用结构一个有结构的类别最初的（或2首字母）学说示例包括置换范畴作为由单个对象生成的自由对称单体范畴，或单纯形范畴这是具有幺半群的幺半群范畴中的初始范畴。

基本概念

类别之间的同态是函子.

这种方式小类别他们自己形成了一个类别猫其对象是小范畴，其态射是函子。这自然会增强到2类谁的2-同构是自然转化s在函子之间。

安范畴的等价性是中的等效项猫，因此有一对函子来回运动，相互逆自然同构.

比表现出等价性的一对函子的概念更弱的是一对伴随函子第条。

类别的其他标准操作包括

• 相反类别

• 本地化

• 范畴的几何实现

相关概念

• 富集类别

  • 连续范畴

• EI-类别

• 0类,（0,1）-类别

• 类别

  半范畴

• 2类

• 3类

• n类

• （∞，0）-范畴

• （n，1）-类别

• （∞，1）-范畴

• （∞，2）-范畴

• （∞，n）-范畴

• （n，r）-类别

工具书类

（有关更多参考，请参阅范畴理论.)

这个概念起源于

• 塞缪尔·艾伦伯格,桑德斯·麦克莱恩,自然等价物通论《美国数学学会学报》582 (1945) 231-294 [doi:10.1090/S0002-9947-1945-00131-6,jstor:1990284]

定义“具有一组形态”（即内部类别在里面设置)出现在：

• 亚历山大·格罗滕迪克，第4节：解构与存在的技巧III：préschémas商《塞米纳伊尔·布尔巴吉：1960年至1961年》，《展览205-222》，《塞米纳伊尔·布勒巴吉》，第6期（1961年），第212期(编号：SB_1960-1961__6__99_0,pdf格式)

教科书帐户：

• 桑德斯·麦克莱恩,数学工作者的范畴，数学研究生课程5施普林格（1971年，第二版，1997年）[doi:10.1007/978-1-4757-4721-8]

• 弗朗西斯·博尔塞克斯,范畴代数手册，数学百科全书及其应用50剑桥大学出版社（1994）

• 罗伊·克罗尔,类型的类别，剑桥大学出版社（1994）[doi:10.1017/CBO9781139172707]

  (范畴语义学属于类型理论)

曝光：

• A.Martini、H.Ehrig和D.Nunes，基本范畴理论的要素柏林技术大学96-5技术报告。

• Jaap van Oosten，基本范畴理论.

• 保罗·佩罗内,用基础数学中的例子说明范畴理论. (arXiv公司)

• Andrea Schalk和H.Simmons，四个简单动作中的范畴理论介绍，作为理科硕士课程的一部分提供的课程笔记。曼彻斯特大学数学逻辑专业。

• 丹尼尔·图里姆，范畴理论课堂讲稿, 1996-2001. 基于Mac Lane的书（1998）。

一本教科书，通过下列实例介绍类别：数学物理是

• 罗伯特·杰罗赫,数学物理芝加哥大学出版社（1985）[国际标准图书编号：9780226223063]

着眼于理论的教科书滑轮类别及其在中的应用同调代数是

• 卡西瓦拉、夏皮拉、，类别和滑轮

中类别的定义基础属于同伦型理论（请参阅同伦类型理论中的内部范畴)在中进行了讨论

• Benedikt Ahrens公司,克里斯·卡普尔金,迈克尔·舒尔曼,单价类别和Rezk完成，《计算机科学中的数学结构》25.5（2015）：1010-1039(arXiv公司：1303.0584)

• 保罗·卡普里奥蒂,尼古拉·克劳斯,通过完备半正则类型的单叶高范畴(arXiv:1707.03693)

• 杰森·格罗斯,亚当·克利帕拉,大卫·斯皮瓦克,在Coq中实现性能类别理论库的经验(arXiv公司：1401.7694)

有关更多参考，请参阅范畴论.