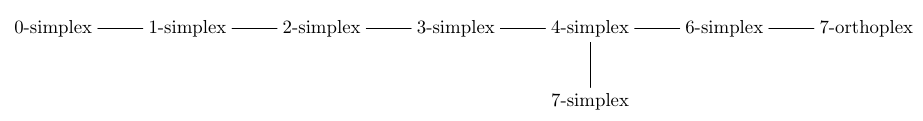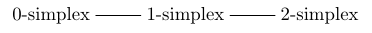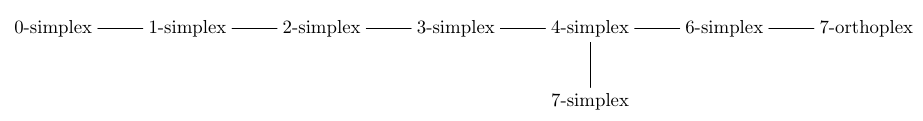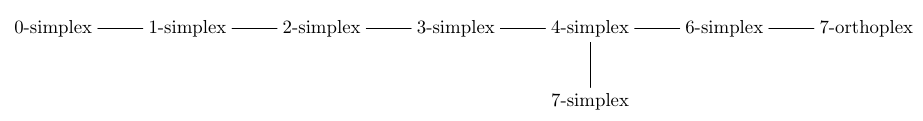积分八元数(第五部分)
2013年9月3日
积分八元数(第五部分)
约翰·贝兹
如果你在8个维度上取一堆大小相等的球,并让尽可能多的球都接触到中心的球,它们的中心将是\(\mathrm)的顶点{E} 8个\)根多面体。这里有两种绘制方法-单击以获取更多信息:
在其8维的辉煌中,这个形状有:
- 240个顶点
- 6720个边缘
- 60480个2d面,均为等边三角形
- 241920个三维面,它们都是正四面体
- 483840个4d面,都是常规的4-simplex
- 483840个5d面,都是常规的5单纯形
- 207360个6d面,都是常规的6-simplex
- 19440个7d面,包括17280个常规7-simplex和2160个常规7-ortholex
和
- 包含696729600个元素的对称组,包括旋转和反射。
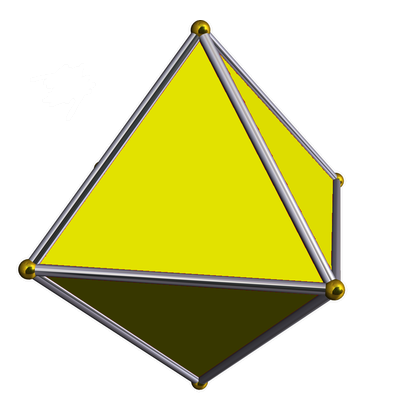
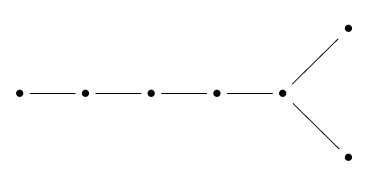
记住,3-单纯形是四面体:
而3-正六面体是八面体:
任何人都可以在上查找这些疯狂的数字维基百科.但我们怎么能看出他们是对的呢?
这是我们今天的挑战。如果我们定义\(\mathrm{E} _8个\)根多面体从这张图片开始:
并使用理论简单的Dynkin图,这是点之间没有任何多条边的Dynkin图。(我将要说的大部分内容都适用于其他Dynkin图,但我将通过关注这个案例来节省一些时间。)
假设我们有这样一个带点的图。在基本层面上,该图告诉我们在(n)维欧几里德空间中取一组单位向量,如果没有边连接它们,则确保它们处于(90°)角,如果有边连接,则确保其处于(120°)角是连接它们的边缘。
我们得到了一个名为根晶格取这些向量的所有整数线性组合。最接近原点的非零矢量称为根这些根是被称为根多面体.
根包括我们开始使用的向量,在Dynkin图中每个点对应一个向量:这些称为简单根。但是还有很多。
以\(\mathrm开头{E} _8个\)Dynkin图,我们可以原则上弄清楚我们想知道的关于\(\mathrm的一切{E} _8个\)根多面体,包括每个维度有多少个面,以及对称群的大小。但要优雅地做这些事情,使用一些技巧会有所帮助。
Coxeter组
主要技巧是使用Coxeter组任何简单的Dynkin图都给出了这样一个组,而且很容易描述。它有一个生成器
$$s_i^2=1$$对于Dynkin图中的每个点,一个关系
$$s_i s_j s_i=s_i s _j s-i$$对于由一条边连接的每对点和一个关系
$$s_i s_j=s_j s_i$$对于每对点不由边缘连接。每个生成器\(s_i \)对应一个反射:将第\(i \)个简单根翻转为负值的反射。
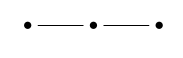
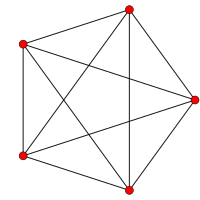
例如,从名为\(\mathrm的Dynkin图开始{A} _3个\):
我们得到了一个有3个生成元的群,它恰好是正四面体的对称群:
所以,你应该把Dynkin图中的三个点想象成代表“顶点”、“边”和“面”。为什么?因为Coxeter组的相应生成器是以下反射:
•切换两个相邻顶点,
•切换两个相邻边,以及
•切换两个相邻面,
分别!
\(\mathrm{A} _n(n)\)图以同样的方式给出了正则单形的对称群。一个类似的故事也适用于规则维正射的对称群,但它的Dynkin图并不是简单的花边,所以我不会深入讨论细节。我们现在真正需要的案例是{E} _8个\)Dynkin图及其子图。
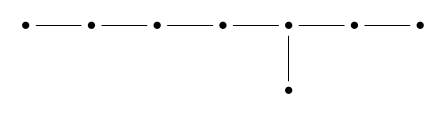
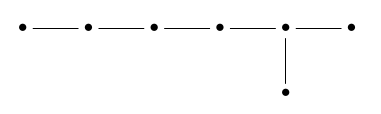
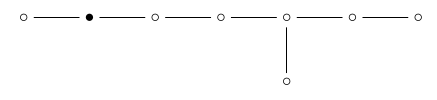
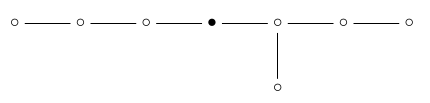
例如,如果我们去掉\(\mathrm)的结束点{E} 8个\)我们得到一个子图,名为\(\mathrm{D} _7个\),如下所示:
或者,在把它整理好之后,这个:
从左到右阅读,可以认为这里的点代表“顶点”、“边”、“2d面”、“3d面”等等……但当我们到达图表的右端时,显然一定会发生一些有趣的事情!
有二表示“顶面”的点。原因是这个Coxeter群是7正射体的对称群,它的6维面交替地被涂上白色和黑色。我们只考虑将脸转换为相同颜色的脸的对称性。两个6d面最多相交一个5d面,因此“5d面”没有点。我们可以这样总结这个故事:
所有\(\mathrm{D} _n(n)\)Dynkin图看起来很相似,一行中有一些点,最后是两个。。。他们都以同样的方式工作。它们的Coxeter群是正交形的对称群,它们的顶维面交替着色为白色和黑色。
如果是\(\mathrm{E} _8个\),发生了更奇怪的事情!顶维面有两种:7-单纯形面和7-正射面:
子图还出现了其他微妙之处{E} _7个\)和\(\mathrm{E} _6个\). 所以,你可能认为这个主题是一个复杂的泥潭。但事实并非如此。
考克塞特复合物
要以系统的方式处理所有的Coxeter群,最好将它们视为某些简单复数的对称群,称为“Coxeter复数”。粗略地说,简单复合体是一种由0-简单体、1-简单体、2-简单体、3-简单体等组成的小工具,所有这些都以一种很好的方式粘在一起。
如果有一个带点的Coxeter图,则其Coxeter复数中单形的最高维是(n-1)。对于Coxeter组的每个元素,都有一个这样的顶级单形。例如,我已经说过这个Dynkin图:
给出了由正四面体对称性组成的Coxeter群,我指的是所有反射和旋转。这个组有4个!=24个元素,因此Coxeter复合体由24个三角形构成。事实上,我们做到了重心细分四面体的表面!我们可以在球体上绘制它,如下所示:
你可以看到有24个三角形。而且,你可以看到,如果你固定一个给定的三角形,Coxeter群会有一个独特的对称性,将其映射到任何其他三角形。
一般来说,带(n)点的Dynkin图的Coxeter群总是充当(mathbb{R}^n)的线性变换。每个根都会产生一个反射,将该根翻转为负值。因此,这个组也作用于(n-1)-球体。如果我们取这个球体,沿着对应于Coxeter组中所有反射的超平面将其切碎,我们得到考克塞特复合物。看看你能否在上图中看到这一点。
更好的是,如果您在Coxeter复数中选择任何一个顶维单纯形,那么Coxeter组中总是正好有一个元素将其映射到任何其他顶维单纯形。因此,考克塞特复合体是由单纯形构成的最好的东西,考克塞特群在单纯形上充当对称!
与Dynkin图相对应的Coxeter组的大小始终是某些整数的乘积,Dynkin图中的每个点对应一个整数。这些整数有很多重要的属性,计算它们确实是我们要解决的所有问题的关键。首先,让我向您展示这些数字以及我们可以用它们做什么。
它们在这里。对于任何Dynkin图\(D\),让\(W(D)\)为其Coxeter群,也称为其Weyl群以下是所有简单的Dynkin图中这些组的大小:
$$\开始{array}{ccll}|W(\mathrm{A} _n(n))|&=&2\cdot 3\cdot 4\cdot\cdots\cdot(n+1)\\|W(\mathrm{D} _n(n))|&=&2\cdot 4\cdot 6\cdot\cdots\cdot 2(n-1)\cdot n&=&(2n)\\|W(\mathrm{E} _6个)|&=&2\cdot 5\cdot 6\cdot 8\cdot 9\cdot 12&=&51840\\\\|W(\mathrm{E} _7个)|&=&2\cdot 6\cdot 8\cdot 10\cdot 12\cdot 14\cdot 18&=&2903040\\|W(\mathrm{E} _8个)|&=&2\cdot 8\cdot 12\cdot 14\cdot 18\cdot 20\cdot 24\cdot 30&=&696729600\end{数组}$$很容易看出,(n)维单纯形的对称群(W(A_n))的大小等于
$$|W(\mathrm{A} _n(n))|=(n+1)$$因为\(n\)-单纯形具有以任何方式排列其顶点的对称性。虽然这不是一个简单的例子,但也很容易看出,维正交的对称群W(B_n)的大小等于
$$|W(\mathrm{B} _n(n))|=2^n个$$这个数字等于双阶乘
$$(2n)!!=2\cdot 4\cdot\cdots\cdot 2n$$最后,也很容易看出,(W(D_n)),即正交形的对称群,其顶维面交替着色为白色和黑色,是其一半大。所以,它的大小是半双阶乘共\(2n\):
$$(20亿)?!=2\cdot 4\cdots\cdot 2(n-1)\cdot n$$所以,唯一的问题是计算\(W(\mathrm{E} _6个)\),\(W(\mathrm{E} _7个)\)、和\(W(\mathrm{E} _8个)\). 我稍后再谈。
你可能会认为我们把这些Coxeter群的大小写成数字的乘积有点武断,但事实并非如此!我将在文章的末尾详细讨论这一点。但这里有一点乐趣:
谜题1。如果你把每个数字加倍,再减去一,然后把结果加起来,你就得到了这个Dynkin图对应的Lie群的维数。为什么?
让我们检查一下它是否适用于\(\mathrm{E} _8个\):
$$2\cdot(2+8+12+14+18+20+24+30)-8=2\cdot 128-8=248$$是的,这是李群的维数{E} _8个\)!
准备计算
假设我们知道所有简单的Dynkin图的Coxeter群的大小,让我们看看是否可以计算出每种类型的面{E} 8个\)根多面体有。
我在中解释了该方法第187周每个Dynkin图\(D\)描述了一种“关联几何体”,其中包含不同类型的图形-点、边、三角形、四面体等等点在Dynkin图中。这些图形可以相互“关联”,例如,三角形可以位于四面体上,每个三角形都有一个基本的关联关系边缘在Dynkin图中。
Coxeter群\(W(D)\)对任何给定类型的图形起传递作用。我们还可以求出保持给定类型图形的\(W(D)\)的子群。为此,我们只需从Dynkin图中删除相应的点,然后得到一个子图(E\subset D\)。那么\(W(E)\subseteq W(D)\)就是我们想要的子组!
因此,给定类型的图形集是(W(D)/W(E))。因此,这类数字的数量是比率
$$\压裂{|W(D)|}{|W$$为了看你是否理解这一点,让我们做一个简单的例子!四面体有多少条边?这里我们的Dynkin图是{A} _3个\):
它描述了一种几何形状,即四面体,具有三种图形:
假设我们想计算1-单形或边的数量。我们采用“1-simplex”点:
然后我们删除它,得到这个子图:
嗯,这没有连接!但没关系。此图是单点Dynkin图的两个副本的不相交并集,\(\mathrm{A} _1个\). 如果你遵循规则,你会看到它的Coxeter组就是产品
$$W(\mathrm{A} _1个)\次W(\mathrm{A} _1个) $$所以,四面体中的边数是
$$\压裂{|W(\mathrm{A} _3个)|}{|W(\mathrm{A} 1个)|\times|W(\mathrm{A} _1个)|} = \裂缝{4!}{2!\乘以2!}=6$$这是对的!
如果你从未做过这类事情,我鼓励你多举一些例子。这很有趣!但是,经过多年的热身锻炼,我现在要去攀登珠穆朗玛峰,数一数各种各样的数字{E} _8个\)根多面体。
一开始很容易,但接近尾声时,就像你从这张照片中想象的那样,它变得很狡猾,我会滑倒的。挂在冰冷的悬崖上,我会寻求你的帮助!
0-单纯形
如果我们从\(\mathrm{E} _8个\)Dynkin图:
我们只剩下\(\mathrm{E} _7个\)
因此,\(\mathrm的顶点数{E} _8个\)根多面体是
$$\开始{数组}{ccl}\frac{|W(\mathrm{E} _8个)|}{|W(\mathrm{E} _7个)|}&=&\frac{2\cdot 8\cdot 12\cdot 14\cdot 18\cdot 20\cdot 24\cdot 30}{2\cdot 6\cdot 8\ cdot 12\ cdot 14\ cdot 18}\\\\&=&\ frac{20\cdot24\cdot30}{6\cdot10}\\\\&=&240\end{array}$$正如我们所知!
只是为了好玩,在下一步的最后一步,我从顶行的大分数中取消了所有的数字。这是值得做的,因为同一个计算的(q)变形版本允许我们计算某个空间中的点的数量,该空间称为“格拉斯曼”(Grassmannian),表示组的版本{E} _8个\)在有限域上用(q)元素定义,其中(q)是任意素数幂。我解释了这是如何在第186周和第187周.
在\(q\)-变形计数中,我们将整数替换为\(q \)-整数,定义如下:
\([n]=1+q+q^2+\cdots+q^{n-1}\)因此,对于这个特殊的格拉斯曼,点的数量是
$$\frac{[2]\cdot[8]\cdot[12]\cdot[14]\cdot[18]\cdot[20]\cdot[24]\cdot[30]}{[2]\cdot[6]\cdot[8]\cdot[10]\cdot[12]\cdot[14]\cdot[18]}$$或者,尽我们所能取消,
$$\压裂{[20]\cdot[24]\cdot[30]}{[6]\cdot[10]}$$信不信由你,这是(q)中的多项式。但我们不能说它等于\([240]\),因为一般来说\([nm]\ne[n][m]\)。只有当我们设置(q=1)时,这个方程才成立,然后我们得到240个点。所以,我们现在的问题,涉及考克塞特集团,涉及到传奇人物的特殊情况,但到目前为止仍然是神话'带有一个元素的字段'.
但如果我们愿意的话,我们可以看看这个组{E} _8个\)用2个元素在字段上定义。它以传递方式作用于具有
$$\压裂{[20]\cdot[24]\cdot[30]}{[6]\cdot[10]}$$点。那是多少分?在这种情况下
$$[n]=1+2+4+\cdots+2^{n-1}=2^n-1$$所以点数是
$$\压裂{(2^{20}-1)(2^}24}-1)293,091,386,578,365,375 $$1-单形
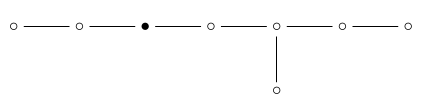
如果我们从\(\mathrm{E} _8个\)Dynkin图:
我们只剩下\(\mathrm{A} _1个\次\mathrm{E} _6个\):
因此,\(\mathrm的边数{E} _8个\)根多面体是
$$\开始{数组}{ccc}\frac{|W(\mathrm{E} _8个)|}{|W(\mathrm{A} _1个)|\times|W(\mathrm{E} _6个)|}&=&\frac{2\cdot 8\cdot 12\cdot 14\cdot 18\cdot 20\cdot 24\cdot 30}{2\次(2\cdot5\cdot 6\cdot 8\ cdot 9\cdot 12)}\\\\&=&\ frac{14\cdot18\cdot20\cdot24\cdot30}{2\cdot 5\cdot6\cdot9}\\\\&=&6720\end数组}$$2-单体
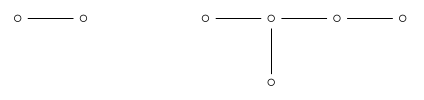
2-单纯形只是一个三角形。如果我们删除“2-simplex”点:
我们只剩下\(\mathrm{A} _2\次\mathrm{D} _5个\):
因此2d面的数量为
$$\开始{数组}{ccc}\frac{|W(\mathrm{E} _8个)|}{|W(\mathrm{A} _2)|\times|W(\mathrm{D} _5个)|}&=&\frac{2\cdot 8\cdot 12\cdot 14\cdot 18\cdot 20\cdot 24\cdot 30}{(2\cdot3)\times(2\ cdot 4\cdot 6\cdot 8\ cdot 5)}\\\\&=&\ frac{12\cdot14\cdot18\cdot20\cdot24\cdot30}{2\cdot3\cdot4\cdot5\cdot6\cdot8}\\\\&=&60480\end{数组}$$3-单纯形
这是一张有趣的3单纯形或四面体的图片。如果我们删除“3-单纯形”点:
我们只剩下\(\mathrm{A} _3个\次\mathrm{A} _4个\):
所以3d面的数量是
$$\开始{数组}{ccc}\frac{|W(\mathrm{E} _8个)|}{|W(\mathrm{A} _3个)|\times|W(\mathrm{A} _4个)|}&=&\frac{2\cdot 8\cdot 12\cdot 14\cdot 18\cdot 20\cdot 24\cdot 30}{(2\cdot3\cdot 4)\times(2\ cdot3\ cdot 4\cdot 5)}\\\\&=&\ frac{8\cdot12\cdot14\cdot18\cdot20\cdot24\cdot30}{2\$$4个单纯形
这是一张4单工的照片。如果我们从\(\mathrm{E} _8个\)Dynkin图:
我们只剩下\(\mathrm{A} 4个\times\mathrm{A} _1个\次\mathrm{A} _2\):
所以4d面的数量是
$$\开始{数组}{ccc}\frac{|W(\mathrm{E} 8个)|}{|W(\mathrm{A} _4个)|\times|W(\mathrm{A} _1个)|\times|W(\mathrm{A} _4个)|}&=&\frac{2\cdot 8\cdot 12\cdot 14\cdot 18\cdot 20\cdot 24\cdot 30}{(2\cdot3\cdot 4\cdot 5)\times 2\ times(2\ cdot 3)}\\\\&=&\ frac{8\cdot12\cdot14\cdot18\cdot20\cdot24\cdot30}{2\cdot2\cdote3\cdot4\cdot5}\\&=&483840\end{array}$$5个单纯形
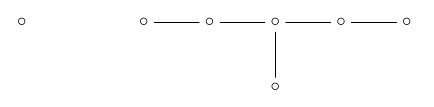
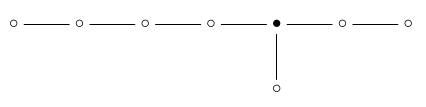
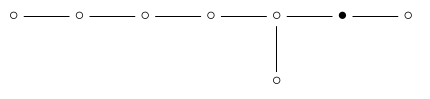
在这一点上,我们遇到了一个谜:在\(\mathrm中没有“5-单纯形”点{E} _8个\)Dynkin图!
这有点像在\(\mathrm中没有5个单纯形点{D} _7个\)Dynkin图:
这里的解决方案是,如果我们有一个“完整的旗帜”,由图片中显示的每种图形组成,所有事件都有一个独特的5-simplex,这是所有其他数字都会遇到的问题。事实上,最多有一个5单纯形与任何由白色和黑色6单纯形组成的对接触。因此,5单工是“多余的”。
我认为,同样的决议必须适用于{E} _8个\). 详细了解这一点将是对我们理解力的一个很好的测试。但让我们继续前进!
6个单纯形
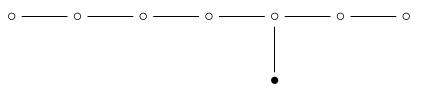
如果我们删除“6-单工”点:
我们只剩下\(\mathrm{A} _6个\次\mathrm{A} _1个\)以下为:
因此6d面的数量显然是:
$$\开始{数组}{ccc}\frac{|W(\mathrm{E} _8个)|}{|W(\mathrm{A} _6个)|\times|W(\mathrm{A} _1个)|}&=&\ frac{2 \cdot 8 \cdot 12 \cdot 14 \cdot 18 \cdot 20 \cdot 24 \cdot 30}{(2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7)\times 2}\\&=&\ frac{8 \cdot 12 \cdot 14 \cdot 18 \cdot 20 \cdot 24 \cdot 30}{2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7}\\&=&69120\end{array}$$但这与维基百科的答案不一致!它说我们的多面体有207360个6维面,都是常规的6单纯形。因此,我们手头有另一个谜团,我们将回到这里。
7个单纯形
如果删除“7-simplex”点:
我们只剩下\(\mathrm{A} _7个\):
因此,7维单纯形面的数量为:
$$\开始{数组}{ccc}\frac{|W(\mathrm{E} _8个)|}{|W(\mathrm{A} _7个)|}&=&\frac{2\cdot 8\cdot 12\cdot 14\cdot 18\cdot 20\cdot 24\cdot 30}{2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7\cdot 8}\\\\&=&\ frac{12\cdot14\cdot18\cdot20\cdot24\cdot30}{3\cdot4\cdot5\cdot6\cdot7}\\\\&=&17280\end{数组}$$7-矫形
如果我们删除“7-oproflex”点:
我们只剩下\(\mathrm{D} _7个\):
因此,7维正射面的数量为:
$$\开始{数组}{ccc}\frac{|W(\mathrm{E} _8个)|}{|W(\mathrm{D} _7个)|}&=&\frac{2\cdot 8\cdot 12\cdot 14\cdot 18\cdot 20\cdot 24\cdot 30}{2\cdot 4\cdot 6\cdot 8\ cdot 10\cdot 12 \cdot 7}\\\\&=&\ frac{12\cdot14\cdot18\cdot20\cdot24\cdot30}{4\cdot6\cdot7\cdot 10\ cdot 12}\\\\&=&2160\end{array}$$但我们还有更多的谜团要解决。
6个单纯形,重新访问
首先,我们的计算似乎显示了\(\mathrm)根多面体的6个单纯形面的数量{E} _8个\)是69120,而维基百科说答案是207360。幸运的是,我们可以用另一种方法来计算答案,这为这个问题提供了一些线索。
我们的多功能镜有17280张7单纯形脸和2160张7矫形脸。每个7单纯形有8个面,都是6单纯形。每个7-矫形肌有2个7面,都是6个单纯形。因此,我们可以天真地计算6个单纯形的总数,并得到
17280美元\cdot 8+2160\cdot 2^7=138240+276480=414720$$但这是双重计数,因为每个6-单纯形都会碰到两个7-单纯形。(凸多面体的顶维面总是成对地沿着次高维面相交。)所以实际数是这个数的一半:
$$\压裂{138240}{2}+\压裂{276480}{2{=69120+138240=207360$$这与维基百科上的答案相符。但它也揭示了我们的错误答案。我们的错误答案是69120,这正是所有7个单纯形的人脸总数。它也是一半这7个矫形肌的总面数。这也是正确答案的1/3!
所有这些都表明,我们的多面体的6个单纯形面有两种,它们不能被多面体对称性互换。其中1/3是我们统计的,即图中提到的类型:
其中2/3是其他类型的6个单纯形,在上图中没有出现。
如果这看起来很奇怪,请记住这个图也不包括我们的多边形的5个单纯形面!还要记住\(\mathrm{D} _7个\)图对应于7-正交,给出了另一个例子,其中一些单纯形有两种,而另一些则根本不出现,即使它们作为7-正交的面存在:
即使这是真的,也显然不足以完全理解。如果我们的多面体有两种6单纯形面,它们有什么不同?数字1/3从哪里来?
这是我的猜测。我们的多面体的7个正射面有6个单纯形面,可以用白色和黑色交替着色,而我们的多面体的所有对称性都保留了这两种颜色。作为证据,请注意,保留7个正入射面的对称性构成了组{D} _7个\),它保留了这种双色。但我猜我们可以用一致的方式进行这种双色,所以我们多边形中的每一个6单纯形要么是白色要么是黑色。
我想我们可以这样做,这样每个7-骨节都能接触到另一个7-矫形在其每个黑色面,和7-单工在其每个白色面孔!另一方面,每一个7-单纯形都被7-正骨所包围。
如果我们能做到这一点:
所有这些都很吻合。。。所以虽然我还没有证明我相信,这种“一致双染色”的存在,以及6个单形和6个正形的排列。
谜题2。在这里证明或反驳我的猜测!
5个单纯形,重新访问
为什么我们的多面体有(483840)个5d面,它们都是常规的5单形?我还没想好怎么数数。有了工作,我应该能够用上一节中的猜测来做这件事,但我只是在几分钟前做了这些猜测。
值得注意的是,\(483840\)也是4d面的数量。
谜题3。演示如何计算\(\mathrm的5d面{E} _8个\)根多面体。
神奇的数字
我所有的计算都依赖于我理解的一般结果,以及一些我不理解的数字:
$$\开始{array}{ccll}|W(\mathrm{E} _6个)|&=&2\cdot 5\cdot 6\cdot 8\cdot 9\cdot 12&=&51840\\\\|W(\mathrm{E} _7个)|&=&2\cdot 6\cdot 8\cdot 10\cdot 12\cdot 14\cdot 18&=&2903040\\\\|W(\mathrm{E} 8个)|&=&2\cdot 8\cdot 12\cdot 14\cdot 18\cdot 20\cdot 24\cdot 30&=&696729600\end{array}$$事实上,在我的计算中,我只需要知道这三个Coxeter群的大小,但尝试理解可以乘法得到它们大小的“幻数”是不可抗拒的。
谜题4。计算这些神奇数字的最佳方法是什么?
返回第186周和第187周,我给出了这些数字的许多特征。不幸的是,它们似乎不容易计算\(\mathrm)的这些数字{E} _6个,\mathrm{E} _7个\)和\(\mathrm{E} _8个\).
我打赌有人知道一个简单的方法。但为了帮你解决这个难题,我会告诉你八个坚硬的方式!
从任何Dynkin图开始,不一定是简单的。设\(G(\mathbb{F})\)是域\(\mat血红蛋白{F}\)上对应的简单代数群。特别地,
$$G=G(\mathbb{C})$$是一个复杂的李群。假设图(D)有点。然后幻数\(d_1,\dots,d_n)是自然数
$$|W(D)|=D_1\cdot\cdots\cdot D_n$$此外:
- (G)的真正上同调是关于生成器(x_1,dots,x_n)的外部代数,Dynkin图中的每个点对应一个代数。这些生成器的度都是奇数,而(x_i)的度是(2d_i-1)。
- 分类空间(BG)的实上同调是生成元(y_1,dots,y_n)上的多项式代数。这些生成器的度数都是偶数,而(y_i)的度数是(2d_i)。
- Weyl群(W(D))作用于(mathbb{R}^n)。该群作用下不变的(mathbb{R}^n)上多项式的代数是生成元(z_1,dots,z_n)上的自由交换代数。多项式(z_i)是次(d_i)的齐次多项式。
- 定义q个-多项式Dynkin图(D)的多项式为(q),其中系数为旗帜品种\(G/B\)。这里\(B\)是Borel子群的\(G\),以及布鲁哈特分解是将\(G/B\)写成\(k\)-单元格不相交并集的标准方式,即\(mathbb{C}^k\)的副本。那么,\(q\)-多项式等于$$[d_1]\cdot\cdots\cdot[d_n]$$其中\([di]=1+q+\cdots+q^{di}\)。
- 如果(q)-多项式中的系数为(d),则(G/B)的第(2i)个同调群为(mathbb{Z}^d)
- 当\(q\)是素数幂时,\(q\)-多项式的值是\(G(\mathbb)的基数{F} (_q))/B(\mathbb{F} (_q))\). 此处\(\mathbb{F} (_q)\)是包含\(q\)元素和\(B(\mathbb)的字段{F} (_q))\)是简单代数群的Borel子群{F} (_q))\).
- 多项式中的系数是长度为(k)的Coxeter群元素的个数。这里是长度当我们将其写为Dynkin图中与点对应的生成器的乘积时,Coxeter群中任何元素的最小长度都是它作为单词的最小长度。
- 多项式中的系数是与Coxeter复数中选定的顶维单纯形的距离为(k)的顶维单形的数量。在这里,我们以一种希望显而易见的方式,根据你需要跨越多少堵墙才能从一堵墙到达另一堵墙,来测量顶级维度单体之间的“距离”。
如果你知道足够多的东西,你可能会很高兴证明所有这些神奇数字的描述都是等价的。
我还没有使用这些神奇数字的描述来解决这个问题:
谜题5。为什么Dynkin图中的这些神奇数字序列是“对称的”?
要解释我在这里的意思,请看\(\mathrm的幻数之间的间距模式{E} _6个\):
$$\开始{数组}{ccccccccc}2&&5&6&&8&9&&12\\\bullet&\circ&\cirk&\bullet&\bullet&\cick&\bullt&\bullat&\pirc&\built\end{array}$$当你反思时,它不会改变!对于\(\mathrm也是如此{E} _7个,\mathrm{E} _8个\)还有非特殊情况,如果你按递增顺序写幻数。为什么?这让人想起庞加莱的二元性,但我不知道它是怎么回事是那个。
谜题1。如果将每个幻数加倍,再减去一,然后将结果相加,就得到了对应于这个Dynkin图的Lie群的维数。为什么?
回答。汉弗莱的书中有一个自足的证据反射组和Coxeter组; 见定理3.9。就我个人而言,我更喜欢使用这样一个事实,即对应于Dynkin图的Lie群(G)的真正上同调是度(2d_I-1)的生成器(x_I)上的外部代数。因此,\(G\)的上同调中的最高阶元素是乘积\(x_1\cdots x_n\),它具有阶\(\sum_{i=1}^n(2d_i-1)\)。但在(G)的上同调中可能的最高程度只是(G)维度。
谜题2。显示\(\mathrm{E} _8个\)多面体可以交替使用2种颜色,这样他们的黑色脸就可以接触到其他7个直方体,而白色脸可以接触到7个单纯形。
回答。莱拉·伊德拉尼回答说:
你可以通过例子来证明这件事,或者至少我这样做了。
让我们的顶点
$(\pm 1,\pm 1,0,0,0,1,0)$$和排列,以及
$(\pm 1/2,\pm 1/2,\pm1/2,\pm2 1/2,\p.1/2,\ pm 1/2$$对于偶数\(-1/2\)s,我们得到一对顶点通过边连接,当它们的内积为1时。
我们可以看一下以下矫形:
$$(1,1,0,0,0,0,0,0) $$$$ (1,0,1,0,0,0,0,0) $$$$ (1,0,0,1,0,0,0,0) $$$$ (1,0,0,0,1,0,0,0) $$$$ (1,0,0,0,0,1,0,0) $$$$(1,0,0,0,0,0,1,0) $$$$ (1,0,0,0,0,0,0,1) $$$$ (1,-1,0,0,0,0,0,0) $$$$ (1,0,-1,0,0,0,0,0) $$$$ (1,0,0,-1,0,0,0,0) $$$$ (1,0,0,0,-1,0,0,0) $$$$ (1,0,0,0,0,-1,0,0) $$$$ (1,0,0,0,0,0,-1,0) $$$$ (1,0,0,0,0,0,0,-1) $$现在,我们计算出通过添加另一个顶点,哪一组七可以扩展为一个单纯形。
考虑一个顶点\((1,-1,0,0,0-0,0.0)\)。对于另一个具有边的顶点,即具有内积1,其第一个条目必须是正或0,其第二个条目必须是负或0,因为否则内积中将存在负项;两个条目都不能为0,如果两者都为非零,则它们必须分别为1/2和-1/2。
类似地,对于正交形中的任何其他顶点,连接到(v)的任何顶点(w)必须与(v)两个非零项中的一个中的符号匹配,或(w)两者都必须匹配,并且其所有坐标必须为1/2。我们在我们的正交形中取一组七个顶点,这样除了第一个条目外,如果(v)在某处有一个非零条目,那么其他六个顶点在那里有0。这些都是我们的正态集合中的6维单形,因为任何其他集合都会包含一对顶点,其内积为0。假设其中,从1到(k)的\({v_i\}\)在位置\(i\)中都有一个-1。坐标-1/2位于位置\(i),1/2位于所有其他位置的点与给定的所有顶点的距离为2。这样的点是一个顶点,当(k)是偶数时。因此,我们得到了64个6-单形,这些6-单形可以扩展到7-单形。此外,这些6个单形与其余的6个单体交替使用,因为给定一个6个单纯形,其中的顶点数为偶数,其中有-1,改变任何顶点,使我们在正射函数中仍然得到6个单形体,就会产生一个6单形,其中顶点数为奇数,其中的-1,反之亦然。现在我们只需要说明,其他64个6单纯形并没有扩展到7单纯形。考虑一组由正射函数中的七个顶点组成的集合,其中奇数的条目为-1,七个顶点形成一个6单纯形。
假设我们有一个顶点\(w\),其条目为0。如果它的第一个条目是1,那么它必须在其他地方有一个条目1或-1,因此它要么与我们的6单纯形中的顶点匹配,要么与之正交。如果\(w)的第一个条目为0,那么它必须在其他两个位置具有非零条目,但由于还有五个剩余条目,因此在我们的6单纯形中,有一个顶点在这两个位置为0,因此与\(w\)正交。如果\(w)只有\(\pm 1/2)的条目,那么它必须匹配单纯形中的每个顶点,只要该单纯形不为零,但这样做会产生条目数为-1/2的奇数点,这不是一个顶点。因此,这6个单体不能扩展到7个单体,因此必须连接到正骨(正骨片?)。
所以这个特殊的直视镜有其6个面中的一半与单纯形相连,另一半与其他直视镜相连,这样的面是交替的。通过对称性,这适用于所有矫形。
谜题3。演示如何计算\(\mathrm的5d面{E} _8个\)根多面体。
回答。Layra Idrani在维基百科上解释了答案:
就5个单纯形而言,我认为最快的方法是计算每个7个单纯色的5个单数(28),然后乘以7个单数的数量(17280)。这给出了正确的答案(483840)。现在我们只需要证明这是正确的计算。
我们知道,我们只需要担心包含在7个单形中的5个单形,因为对于正射中的任何5个单体,它都可以扩展到白色的6个单形。
为了证明每个5单纯形都是一个唯一的7单纯形,我们来看4单纯形。根据该图,每个4单纯形A正好包含在两个7单纯形中,分别表示为B和C。因此,如果5单纯形D包含A,则它只能包含在B或C中,而不能包含其他7单纯体,并且实际上必须包含在B和C中的至少一个中。由于所有5单纯体都是相同的,如果任何5单纯色都包含在两种7单纯色中,每个5单纯形必须是两个7单纯形。
所以我们假设D同时在B和C中。由于任何其他包含A的D'必须在B或C中,并且D是两个单形,D'也必须在B和C中。我们知道D'存在,因为B有多个不在A中的顶点。
D和D'共享5个顶点,并且都在同一个7-单纯形B中,因此共同定义了一个唯一的6-simplex,并且6-simple包含在B中。但根据假设,它们也都在C中,所以相同的6-silvlex也在C中。因此我们得到B和C共享一个6-simpler,这是不可能的。
因此D正好位于B和C中的一个,类似地,每个5-单形也正好位于一个7-单形中。
这个答案中我唯一没有理解的部分是,为什么每一个4单纯形都存在于两个7单纯形中。然而,我能够通过对本文中已经使用的技术的一点扩展来确认这一点。
首先我将计算由一个4单纯形和一个包含它的7单纯形组成的对。然后我将计算4单纯色。然后我将第一个数字除以第二个数字,得到2。
为了计算由4-单纯形和包含它的7-单纯形组成的对,我在Dynkin图中标记这些点:
然后将其移除:
给我留下了\(\mathrm的Dynkin图{A} _4个\次\mathrm{A} _2\). 所以,这些对的数量是$$\begin{array}{ccl}\frac{|W(\mathrm{E} _8个)|}{|W(\mathrm{A} _4个)|\times|W(\mathrm{A} _2)|\times|W(\mathrm{A} _4个)|}&=&\frac{2\cdot 8\cdot 12\cdot 14\cdot 18\cdot 20\cdot 24\cdot 30}{(2\cdot3\cdot4\cdot 5)\次(2\次3)}\end{array}$$另一方面,我已经计算了4个单纯形的数量。但提醒一下:要做到这一点,我们只需从Dynkin图中删除4个单纯形点:
留给我们\(\mathrm{A} _4个\次\mathrm{A} _1个\次\mathrm{A} _2\):
所以4d面的数量是$$\开始{数组}{ccl}\frac{|W(\mathrm{E} _8个)|}{|W(\mathrm{A} _4个)|\times|W(\mathrm{A} _1个)|\times|W(\mathrm{A} _4个)|}&=&\frac{2\cdot 8\cdot 12\cdot 14\cdot 18\cdot 20\cdot 24\cdot 30}{(2\cdot3\cdot 4\cdot 5)\times 2\times(2\cdot 3)}\end{array}$$你可以看到这是我们之前答案的一半。所以,是的:有两个7单纯形包含每个4单纯形!
谜题4。对于给定的Dynkin图,计算幻数的最佳方法是什么?
回答。汉弗莱的书中有两种方法,都相当惊人反射组和Coxeter组第一种方法依赖于他的3.20号提案。如果\(h\)是Dynkin图\(D\)的Coxeter数,并且\(1\lem\leh\)相对素数为\(h~),那么\(m+1)是\(D~)的幻数。
回想一下科克塞特数是根数除以Dynkin图中的点数。(有关其他更多概念性描述,请单击链接!)
要使用这个命题,知道根的数目是李代数的维数,对应于(D)减去(D)中的点数。例如,李代数的维数{E} _8个\)是248,它的Dynkin图有8个点,所以根的数目是(248-8=240)(我们已经知道了),它的Coxeter数是(240/8=30)。1到30之间相对素数为30的数字为:$$ 1, 7, 11, 13, 17, 19, 23, 29 $$
所以,加一,我们得到了\(\mathrm)的一些神奇数字{E} _8个\):
$$ 2, 8, 12, 14, 18, 20, 24, 30 $$但其中有八个,在Dynkin图中每个点都只有一个幻数,所以这些必须是全部的神奇的数字!
这就是黑魔法,即使是平时沉默寡言的汉弗莱也会给它打上惊叹号。
顺便问一下,你注意到这些数字有什么有趣的地方吗
$$ 1, 7, 11, 13, 17, 19, 23, 29 ? $$除了1以外,它们都是顶级的!30恰好是最大的数,除了1之外,所有比它小的数和它相对的质数都是质数。我不知道这在这里是否重要,但这真的很可疑。
对于\(\mathrm{E} _7个\)我们必须更加努力。李代数的维数{E} _7个\)是133,所以根的数目是\(133-7=126\),而考克塞特数是\(126/7=18\)。以下是小于18的相对素数为18的数字:$$ 1, 5, 7, 11, 13, 17 $$加一,我们得到\(\mathrm的神奇数字{E} 7个\)以下为:$$ 2, 6, 8, 12, 14, 18 $$不幸的是,这样我们只能得到七个幻数中的六个。幸运的是,汉弗莱斯还证明了神奇数字的序列必须是“对称的”,如拼图5所述。唯一的可能是第七个幻数是10:$$\开始{数组}{ccccccccCCc}2&&&&6&&8&&\mathbf{10}&&12&&14&&&18\\\子弹头$$顺便问一下,你注意到这些数字有什么有趣的地方吗$$ 1, 5, 7, 11, 13, 17 ?$$
是的,它们都是黄金。像30,18是一个非常整数,这意味着每个自然数相对于它都是质数,而小于它的自然数则是1或质数。
对于\(\mathrm{E} _6个\)我们必须更加努力地做晚饭,但我会把这当作一个谜留给你!为了让您开始,我将提醒您{E} _6个\)是78,所以根的数目是\(78-6=72\),所以考克塞特数是\(72/6=12\)。另外:拼图1可能会派上用场。
(顺便说一下,唯一的整数是$$ 1, 2, 3, 4, 6, 8, 12, 18, 24, 30 $$在这次讨论中,他们中的三个人出现了,这对我来说是一个谜。但很容易看出,没有比(30)大的整数。首先,它必须能被(2,3)和(5)整除,否则这两个素数的乘积将相对这个数是素数,并且小于它,但不是素数。所以第一个选项是\(60\)\(60)不是很圆,因为(7^2)相对来说是质数,但不是质数。简而言之,问题是有一个素数不除(60),它的平方小于(60)。因此,任何大于\(30)的整数实际上也需要被\(7)整除,这意味着它必须大于\(2乘3乘5乘7=210)。但是\(11^2<210)和\(13^2<210\),所以任何大于\(30)的整数实际上都必须大于\(2乘3乘5乘7乘11乘13)。以此类推:这显然是一场失败的战斗。在这个阶段,知道在(n)和(2n)之间总是有一个素数就足以保证我们可以通过归纳法来保持这个论点。)
计算幻数的第二种方法更加系统化。
此方法使用高度正根,表示展开为简单根的线性组合时其系数的总和。要计算幻数,您需要计算每个高度有多少个正根,并使用它来获得正根总数的分区。例如,\(\mathrm{B} 2个\)有高度1的2个正根,高度2的1个正根和高度3的1个负根,所以我们得到了分区(2,1,1)。
然后将此分区写为Young图:
XX年X(X)X(X)
然后是你反映这个Young图沿着对角线另一个Young图表:
XXX(XXX)X(X)
然后你读这作为一个分区,即(3,1)。最后,你给每个数字加一,你就得到了神奇的数字!对于\(\mathrm{B} _2\)你得到(4,2)。但该过程通常适用于任何Dynkin图。这听起来很疯狂,但这是真的!这是汉弗莱书中的定理3.20,这是书中的最后一个定理。
谜题5。为什么任何Dynkin图的幻数序列都是“对称的”?
回答。Allen Knutson建议查阅Humphreys的书反射组和Coxeter组本·韦伯斯特说:艾伦是正确的;这种对称性是汉弗莱的引理3.16。快速的解释是,对于特定的单位根,(zeta{d_i-1}是Coxeter元素的特征值集。因为这是一个实矩阵,所以它的特征值是复共轭对。这里\(h\)是Coxeter数Coxeter元素.
你也可以阅读评论上n个-品类咖啡馆,并在那里发表自己的意见或提出问题!
©2013 John Baez版权所有
baez@math.removethis.ucr.andis.edu
家