第37讲-类别介绍第37讲-类别介绍
上次我们看到,对于任何图(G),在该图上都有一个自由范畴,其对象是(G)的节点,其形态是(G\)中的路径。
我们可以使用另一个技巧获得更多的类别:我们可以在图中的路径之间添加方程,但仍然可以获得一个类别!我们只是当两个路径\(f\)和\(g\)为平行,表示某些对象\(x\)和\(y\)的\(f:x\至y\)和(g:x\到y\)。
例如,上次我们看到来自此图的类别:
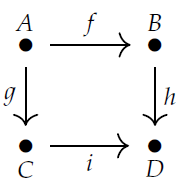
该类别称为方形上的自由类别。在这个类别中,有两条从\(A\)到\(D\)的路径,即\(h\circ f\)和(i\circe g\)。他们不平等!
但我们可以建立一个新的更小的类别,在这里我们人为地规定了(h\circ f=i\circg)。这个类别很有名:它被称为交换平方因为你可以先往下走,然后向右走,从(A\)到(D\),或者向右走,然后往下走,我们将这些计算为同一态射.
这两个类别都很重要。想象一下,住在一个有单行道的城市街区。你住在\(A\),你想去拜访你在\(D\)的朋友。出于某些目的,你走哪条路线可能很重要。然后你应该使用广场上的免费类别。但出于其他目的,这可能无关紧要——你可能不在乎怎样您将从\(A\)到\(D\),只需你是否能做到.那么你应该使用可交换平方!
从以下位置记住第35讲一个预序可以看作是一个从任何对象到任何对象最多有一个态射的范畴。交换平方是一个很好的例子:在交换平方中,从任何对象(a,B,C,D)到任何其他对象最多有一个态射。当我们不在乎时,我们会使用预购单怎样我们从一个物体到另一个物体,只是是否你可以。
的确,我们可以随时任何类别\(\mathcal{C}\)并人为地加入了如此多的方程,以至于我们将其分解为一个预定的序列!这是的主题拼图103。要做到这一点,我们只需说,只要我们有任何形态\(f,g:x\到y\),其中\(x\)和\(y\)是任何在我们的类别中,我们命令\(f=g\)。结果称为\(\mathcal{C}\)的预序反射.
Fong和Spivak在第3.2.3节中讨论了这一点,他们提出了一个很好的观点:图上的自由范畴与预订单非常不同。图上的自由类别具有尽可能少平行态射之间的方程,而预序具有最有可能。
总之,我们通过先在图上取自由范畴,然后在并行态射之间施加一些等式来建立范畴的技巧称为呈现一个类别。该图与方程一起被称为演示类别的。
如果我们使用有限图和有限多个方程,我们会得到一个有限呈现范畴。这些对数据库很重要。
例如,考虑下图:
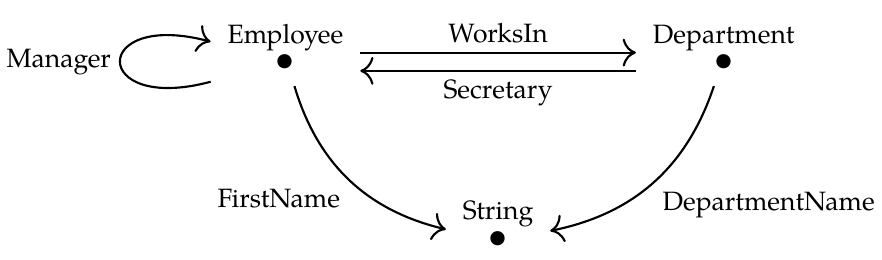
它有3个节点:Employee、Department和String。它有5个边缘:WorksIn、Secretary、DepartmentName、FirstName和Manager。如果你仔细想想,你就会知道发生了什么。每个员工都有一个名字,这是一个字符串,这就是为什么我们有一个从employee到string的边FirstName。在图的自由类别中,这个边给出了一个态射
[\textrm{FirstName}:\textrm{Employee}\to\textrm}String}。]
其他边也是如此。每个部门都有一个秘书,秘书是一名员工,等等
[\textrm{FirstName}\circ\textrm{Manager}\cic\textrm}经理}:\textrm[Employee}\to\textrm{String}]
这表示某个员工经理的名字是字符串!
我们下次再看看这些东西有什么用。但我们并不真的想在这个图上使用免费类别,因为可能会有一些有趣的态射之间的方程.
谜题106。我们可能想要在形态之间强加什么合理的方程式?
我们将看看如何处理得到的有限呈现类别!或者你可以“作弊”并阅读这本书。
如果你这样做了,我应该警告你,当我在为语态合成(f:x\ to y\)和(g:y\ to z\)写(g:x\ toz\)时,Fong和Spivak写(f.g:x\)。这两种约定都很有用。
今天的演讲已经够多了!我再给你留下两个谜题。
拼图107。在此图上选择免费类别:

然后施加等式(s\circ-s\circ-s\ circ-s=1_z\)。您将获得一个包含一个对象的类别,也称为单胚的。这个类别有多少个态射?它与下面的图片有什么关系?

谜题108。取此图上的免费类别:
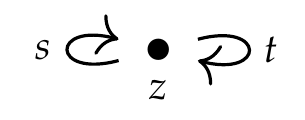
然后将方程
[s\circ s\circs \ circ s=t\circ t=s \circ t\circs \cic t=1_z。]
你又得到了一个幺半群。它与下面的图片有什么关系?
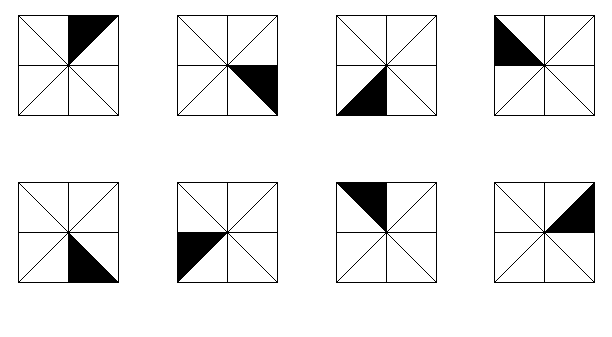
这两个谜题与难题99和100.好好想想!
阅读其他讲座请到这里。
©2018 John Baez版权所有

















